��Ŀ����
16����ԲC��������ԭ�㣬����F1��F2��x���ϣ���Բ�ϵĵ㵽��F1�ľ�������ֵΪ8����F1��ֱ�߽���ԲC��A��B���㣬�ҡ�ABF2���ܳ�Ϊ20������ԲC�ķ���Ϊ��������| A�� | $\frac{y^2}{25}+\frac{x^2}{16}=1$ | B�� | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | C�� | $\frac{x^2}{25}+\frac{y^2}{9}=1$ | D�� | $\frac{x^2}{16}+\frac{y^2}{9}=1$ |
���� ����������Բ����Ϊ��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1\\;��a��b��0��$��a��b��0����a+c=8����ABF2���ܳ�Ϊ4a=20�����a��b�����ɵõ�������Բ���̣�
��� �⣺����������Բ����Ϊ��$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1\\;��a��b��0��$��a��b��0����
����Բ�ϵĵ㵽��F1�ľ�������ֵΪ8����a+c=8��
�ߡ�ABF2���ܳ�Ϊ20����4a=20����a=5��c=3��b=4��
����ԲC�ķ���Ϊ$\frac{{x}^{2}}{25}+\frac{{y}^{2}}{16}=1$����ѡ��B��
���� ���⿼������Բ�ķ��̼����ʣ������е��⣮

��ϰ��ϵ�д�
�����Ŀ
7���ܳ�Ϊ9��Բ�Ľ�Ϊ1rad���������Ϊ��������
| A�� | $\frac{9}{2}$ | B�� | $\frac{9}{4}$ | C�� | �� | D�� | 2 |
4�������ĸ������У�
�١��ȱ������ε������ڽǾ�Ϊ60�㡱�������⣻
�ڡ���k��0����x2+2x-k=0��ʵ������������⣻
�ۡ�ȫ�������ε������ȡ��ķ����⣻
�ܡ���ab��0����a��0���ķ����⣮
���������������ǣ�������
�١��ȱ������ε������ڽǾ�Ϊ60�㡱�������⣻
�ڡ���k��0����x2+2x-k=0��ʵ������������⣻
�ۡ�ȫ�������ε������ȡ��ķ����⣻
�ܡ���ab��0����a��0���ķ����⣮
���������������ǣ�������
| A�� | �ڡ��� | B�� | �ۡ��� | C�� | �١��� | D�� | �١��� |
11���躯�� $f��x��=\frac{2}{x}+lnx$��������
| A�� | $x=\frac{1}{2}$ Ϊ f��x���ļ���ֵ�� | B�� | $x=\frac{1}{2}$Ϊf��x���ļ�Сֵ�� | ||
| C�� | x=2 Ϊ f��x���ļ���ֵ�� | D�� | x=2Ϊf��x���ļ�Сֵ�� |
19���Ȳ�����{an}�У�a4=4��a3+a8=5����a7=��������
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
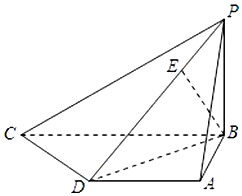 ��֪����P-ABCD�У�����ABCD��ֱ�����Σ�AD��BC��AB��BC��AB=AD=1��BC=2����PB��ƽ��ABCD����PB=1����E����PD�ϣ���BE��PD��
��֪����P-ABCD�У�����ABCD��ֱ�����Σ�AD��BC��AB��BC��AB=AD=1��BC=2����PB��ƽ��ABCD����PB=1����E����PD�ϣ���BE��PD��