题目内容
3.已知函数f(x)=$\left\{\begin{array}{l}{sinx,x≥0}\\{-{x}^{2}-1,x<0}\end{array}\right.$,若f(x)≤kx,则k的范围为( )| A. | [1,2] | B. | [$\frac{1}{2}$,2] | C. | [$\frac{1}{2}$,1] | D. | (-∞,1) |
分析 分类讨论,并分离参数,当x>0时,k≥$\frac{sinx}{x}$,而$\underset{lim}{x→0}$$\frac{sinx}{x}$=1,当x<0时,k≤-x-$\frac{1}{x}$,利用基本不等式即可求出
解答 解:当x=0时,f(0)=sin0=0,k取任何数都成立,
当x>0时,k≥$\frac{sinx}{x}$=1,
当x<0时,k≤-x-$\frac{1}{x}$
∵-x-$\frac{1}{x}$≥2$\sqrt{(-x)•\frac{1}{-x}}$=2,当且仅当x=-1时取等号,
∴k≤2,
综上所述1≤k≤2,
故选:A
点评 本题考查了分段函数的应用以及基本不等式的应用,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
8.已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线平行于直线l:y=x+10,双曲线的一个焦点在直线l上,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | B. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | C. | y2-x2=50 | D. | x2-y2=10 |
13.函数f(x)=$\frac{1}{\sqrt{1-x}}$+$\sqrt{x+3}$-1的定义域是( )
| A. | (-1,3] | B. | (-1,3) | C. | [-3,1) | D. | [-3,1] |
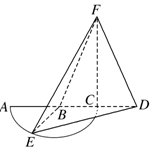 如图,以AC=2为直径的⊙B,点E为$\widehat{AC}$的中点,点D在直径AC延长线上,CD=1,FC⊥平面BED,FC=2.
如图,以AC=2为直径的⊙B,点E为$\widehat{AC}$的中点,点D在直径AC延长线上,CD=1,FC⊥平面BED,FC=2.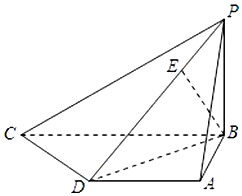 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且BE⊥PD.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且BE⊥PD.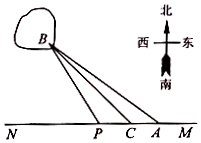 如图,已知A,B两镇分别位于东西湖岸MN的A处和湖中小岛的B处,点C在A的正西方向1km处,tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,现计划铺设一条电缆联通A,B两镇,有两种铺设方案:①沿线段AB在水下铺设;②在湖岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设,预算地下、水下的电缆铺设费用分别为2万元∕km、4万元∕km.
如图,已知A,B两镇分别位于东西湖岸MN的A处和湖中小岛的B处,点C在A的正西方向1km处,tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,现计划铺设一条电缆联通A,B两镇,有两种铺设方案:①沿线段AB在水下铺设;②在湖岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设,预算地下、水下的电缆铺设费用分别为2万元∕km、4万元∕km.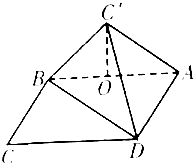 如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.
如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.