题目内容
4.实数2,b,a依次成等比数列,则方程$a{x^2}+bx+\frac{1}{3}=0$的实根个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 0或2 |
分析 由等比数列性质得b=2q,a=2q2,从而方程$a{x^2}+bx+\frac{1}{3}=0$转化为:2q2x2+2qx+$\frac{1}{3}$=0,由此利用根的判别式能求出方程$a{x^2}+bx+\frac{1}{3}=0$的实根个数.
解答 解:∵实数2,b,a依次成等比数列,
∴b=2q,a=2q2
∴方程$a{x^2}+bx+\frac{1}{3}=0$转化为:2q2x2+2qx+$\frac{1}{3}$=0,
∵$△=(2q)^{2}-\frac{8}{3}{q}^{2}$=$\frac{4}{3}{q}^{2}$>0,
∴方程$a{x^2}+bx+\frac{1}{3}=0$的实根个数为2个.
故选:C.
点评 本题考查方程的实根个数的判断,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案
相关题目
19.等差数列{an}中,a4=4,a3+a8=5,则a7=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
16.直线l过抛物线C:y2=4x的焦点F交抛物线C于A、B两点,则$\frac{1}{{|{AF}|}}+\frac{1}{{|{BF}|}}$的取值范围为( )
| A. | {1} | B. | (0,1] | C. | [1,+∞) | D. | $[{\frac{1}{2},1}]$ |
13.函数f(x)=$\frac{1}{\sqrt{1-x}}$+$\sqrt{x+3}$-1的定义域是( )
| A. | (-1,3] | B. | (-1,3) | C. | [-3,1) | D. | [-3,1] |
14.下列表示正确的是( )
| A. | ∅∈{0} | B. | {3}∈{1,3} | C. | 0⊆{0,1} | D. | ∅⊆{2} |
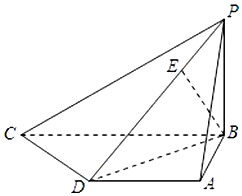 已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且BE⊥PD.
已知四棱锥P-ABCD中,底面ABCD是直角梯形,AD∥BC,AB⊥BC,AB=AD=1,BC=2,又PB⊥平面ABCD,且PB=1,点E在棱PD上,且BE⊥PD.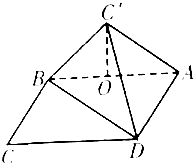 如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.
如图.在矩形ABCD中.AB=3 $\sqrt{3}$,BC=3,沿对角线BD把△BCD折起.使C移到C′.且C′在面ABC内的射影O恰好落在AB上.