题目内容
8.已知O、A、B、C是平面内四点,$\overrightarrow{OC}={sin^2}α\;\;\overrightarrow{OA}+{cos^2}α\;\overrightarrow{OB}$,α是锐角.(1)证明:C在线段AB上;
(2)若α=45°,$|\overrightarrow{OA}|=|\overrightarrow{OB}|=1$,且$|\overrightarrow{OA}-\overrightarrow{OB}|=\sqrt{2}$,求$|\overrightarrow{OC}|$.
分析 (1)利用sin2α+cos2α=1,$\overrightarrow{OC}={sin^2}α\;\;\overrightarrow{OA}+{cos^2}α\;\overrightarrow{OB}$,即可证明C在线段AB上;
(2)由题意,C是AB的中点,由$|\overrightarrow{OA}|=|\overrightarrow{OB}|=1$,且$|\overrightarrow{OA}-\overrightarrow{OB}|=\sqrt{2}$,可得OA⊥OB,即可求$|\overrightarrow{OC}|$.
解答 (1)证明:∵sin2α+cos2α=1,$\overrightarrow{OC}={sin^2}α\;\;\overrightarrow{OA}+{cos^2}α\;\overrightarrow{OB}$,
∴A、B、C共线,且C在线段AB上;
(2)解:由题意,C是AB的中点,
∵$|\overrightarrow{OA}|=|\overrightarrow{OB}|=1$,且$|\overrightarrow{OA}-\overrightarrow{OB}|=\sqrt{2}$,
∴OA⊥OB,
∴$|\overrightarrow{OC}|$=$\frac{1}{2}$|$\overrightarrow{BA}$|=$\frac{\sqrt{2}}{2}$.
点评 本题考查向量知识的运用,考查学生的计算能力,正确运用向量的运算是关键.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案
相关题目
20.在某次测量中得到的A样本数据如下:41,44,45,51,43,49,若B样本数据恰好是A样本数据每个都减5后所得数据,则A,B两样本的下列数据特征对应相同的是( )
| A. | 众数 | B. | 中位数 | C. | 平均数 | D. | 标准差 |
17.下列各式的值为$\frac{1}{4}$的是( )
| A. | $2{cos^2}\frac{π}{12}-1$ | B. | $\frac{{2tan{{22.5}°}}}{{1-{{tan}^2}{{22.5}°}}}$ | ||
| C. | 1-2sin275° | D. | sin15°cos15° |
18.如图,正方体ABCD-A1B1C1D1中,E为CC1中点,则下列结论中不正确的是( )
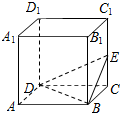

| A. | BD⊥A1C1 | B. | AC1∥平面BDE | ||
| C. | 平面BDE∥平面AB1D1 | D. | 平面A1BD⊥平面BDE |