题目内容
13.抛物线x2=4y的弦AB过焦点F,且AB的长为6,则AB的中点M的纵坐标为2.分析 设A(x1,y1),B(x2,y2),由AB的长为6,|AB|=y1+y2+p,知y1+y2=4,可得A、B中点的纵坐标.
解答 解:设A(x1,y1),B(x2,y2),则
∵AB的长为6,
∴|AB|=y1+y2+2=6
∴y1+y2=4,
∴A、B中点的纵坐标为2.
故答案为:2.
点评 本题考查抛物线的性质和应用,解题时要认真审题,仔细解答,注意公式的合理运用.

练习册系列答案
相关题目
4.抛物线y=$\frac{1}{4}{x}^{2}$的准线方程为( )
| A. | x=-1 | B. | x=-$\frac{1}{16}$ | C. | y=-1 | D. | y=-$\frac{1}{16}$ |
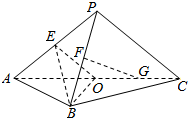 如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.