题目内容
在△ABC中,设角A,B,C的对边分别为a,b,c,且2acosC=2b-c.
(1)求角A的大小;
(2)若a=
,b=4,求边c的大小.
(1)求角A的大小;
(2)若a=
| 21 |
考点:余弦定理的应用
专题:计算题,解三角形
分析:(1)由已知得sinC=2cosAsinC,从而求得cosA=
,结合已知即可求出角A的大小;
(2)由余弦定理即可求得边c的大小.
| 1 |
| 2 |
(2)由余弦定理即可求得边c的大小.
解答:
解:(1)因为2acosC=2b-c,所以
2sinAcosC=2sinB-sinC
=2sin(A+C)-sinC
=2(sinAcosC+cosAsinC)-sinC …4分
即sinC=2cosAsinC,
又因为0<C<π,所以sinC≠0,
所以cosA=
,
又因为0<A<π
所以A=
. …8分
(2)因为a2=b2+c2-2bccosA,即21=16+c2-4c
所以c2-4c-5=0,解得c=-1(舍),c=5. …12分.
2sinAcosC=2sinB-sinC
=2sin(A+C)-sinC
=2(sinAcosC+cosAsinC)-sinC …4分
即sinC=2cosAsinC,
又因为0<C<π,所以sinC≠0,
所以cosA=
| 1 |
| 2 |
又因为0<A<π
所以A=
| π |
| 3 |
(2)因为a2=b2+c2-2bccosA,即21=16+c2-4c
所以c2-4c-5=0,解得c=-1(舍),c=5. …12分.
点评:本题主要考察了余弦定理的综合应用,属于基础题.

练习册系列答案
相关题目
已知函数f(x)=x3-
x2sinθ,其中x∈R,θ为参数,且0≤θ≤π.若函数f(x)的极小值小于-
,则参数θ的取值范围是( )
| 3 |
| 4 |
| 1 |
| 128 |
A、(
| ||||
B、(
| ||||
C、[
| ||||
D、(
|
已知A、B、C三点在球心为O,半径为3的球面上,且三棱锥O-ABC为正四面体,那么A、B两点间的球面距离为( )
A、
| ||
B、
| ||
C、
| ||
| D、π |
已知一个棱长为2的正 方体,被一个平面截后所得几何体的三视图如图所示,则该截面的面积为( )
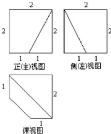

A、
| ||||
| B、4 | ||||
C、
| ||||
| D、5 |
函数f(x)=lnx-
的零点所在的区间是( )
| 3 |
| x |
| A、(1,2) |
| B、(1,e) |
| C、(e,3) |
| D、(e,+∞) |
对于函数f(x)=
,下列命题正确的是( )
|
| A、值域[-1,1] | ||
B、当且仅当x=2kπ+
| ||
| C、最小正周期为π | ||
D、当且仅当2kπ+π<x<2kπ+
|
