题目内容
9.设f(x)=log2(2+|x|)-$\frac{1}{2+{x}^{2}}$,则使得f(x-1)>f(2x)成立的x取值范围是(-1,$\frac{1}{3}$).分析 判断函数的奇偶性,通过x大于0,判断函数是增函数,然后转化求解不等式的解集即可.
解答 解:函数f(x)=log2(2+|x|)-$\frac{1}{2+{x}^{2}}$,是偶函数,
当x≥0时,y=log2(2+x),y=-$\frac{1}{2+{x}^{2}}$都是增函数,所以f(x)=log2(2+x)-$\frac{1}{2+{x}^{2}}$,x≥0是增函数,
f(x-1)>f(2x),可得|x-1|>|2x|,可得3x2+2x-1<0,解得x∈(-1,$\frac{1}{3}$).
故答案为:(-1,$\frac{1}{3}$).
点评 本题考查函数的与方程的应用,函数的奇偶性以及函数的单调性的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
19.实数x,y满足不等式组$\left\{\begin{array}{l}x≥0\\ y≥0\\ x-y-1≤0\\ x-2y+1≥0\end{array}\right.$,则2x-y的最大值为( )
| A. | $-\frac{1}{2}$ | B. | 0 | C. | 2 | D. | 4 |
17.已知A,B,C三点在球O的球面上,AB=BC=CA=3,且球心O到平面ABC的距离等于球半径的$\frac{1}{3}$,则球O的表面积为( )
| A. | 36π | B. | 4π | C. | $\frac{27}{4}$π | D. | $\frac{27}{2}$π |
14.设x,y∈R,a>1,b>1,若ax=by=3,a+b=6,则$\frac{1}{x}$+$\frac{1}{y}$的最大值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
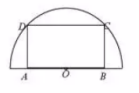 如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、
如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、