题目内容
19.已知函数f(x)=3x-1,x∈{x∈N|1≤x≤4},则函数f(x)的值域为{2,5,8,11}.分析 根据x∈{x∈N|1≤x≤4},确定x的值,可求出函数f(x)的值域.
解答 解:由题意:x∈{x∈N|1≤x≤4}={1,2,3,4}.
函数f(x)=3x-1,
当x=1时,f(x)=2;
当x=2时,f(x)=5;
当x=3时,f(x)=8;
当x=4时,f(x)=11;
∴函数f(x)的值域为{2,5,8,11}.
故答案为:{2,5,8,11}.
点评 本题考查了定义域和值域的求法.比较基础.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若a、b为实数,则“a<1”是“$\frac{1}{a}>1$”的( )条件.
| A. | 充要 | B. | 充分不必要 | ||
| C. | 必要不充分 | D. | 既不充分也不必要 |
17.已知函数$f(x)=\frac{{{x^2}-2x}}{x-2},g(x)=\sqrt{1+x}+\sqrt{1-x}$,下列判断正确的是( )
| A. | 函数f(x)是奇函数,函数g(x)是偶函数 | |
| B. | 函数f(x)不是奇函数,函数g(x)是偶函数 | |
| C. | 函数f(x)是奇函数,函数g(x)不是偶函数 | |
| D. | 函数f(x)不是奇函数,函数g(x)不是偶函数 |
18.设等差数列{an}的前n项和为Sn,且S6=3,S9=45,则S3=( )
| A. | 39 | B. | -39 | C. | 12 | D. | -12 |
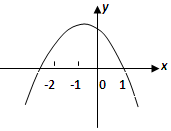 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0; ②b2-4ac>0;③4a-2b+c>0; ④a-b+c<0
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0; ②b2-4ac>0;③4a-2b+c>0; ④a-b+c<0