题目内容
14.设x,y∈R,a>1,b>1,若ax=by=3,a+b=6,则$\frac{1}{x}$+$\frac{1}{y}$的最大值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
分析 根据对数的运算性质和基本不等式即可求出.
解答 解:设x,y∈R,a>1,b>1,ax=by=3,a+b=6,
∴x=loga3,y=logb3,
∴$\frac{1}{x}$+$\frac{1}{y}$=log3a+log3b=log3ab≤log3($\frac{a+b}{2}$)=2,当且仅当a=b=3时取等号,
故选:D
点评 本题考查了不等式的基本性质和对数的运算性质,属于基础题.

练习册系列答案
相关题目
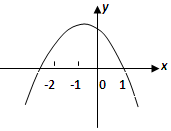 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0; ②b2-4ac>0;③4a-2b+c>0; ④a-b+c<0
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列四个结论:①b<0; ②b2-4ac>0;③4a-2b+c>0; ④a-b+c<0