题目内容
16.方程|x2-y|=1-|y|所表示的曲线是( )| A. |  | B. | 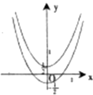 | C. |  | D. | 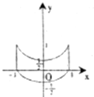 |
分析 易知|y|≤1;从而排除A,B;再分类讨论以确定曲线的形状即可.
解答 解:∵1-|y|≥0,
∴|y|≤1;
故排除A,B;
①当-1≤y≤0时,
|x2-y|=1-|y|可化为x2-y=1+y,
故y=$\frac{{x}^{2}-1}{2}$;
②当0<y≤1,x2<y时,
y-x2=1-y,
故y=$\frac{{x}^{2}+1}{2}$,
故排除C,
故选D.
点评 本题考查分类讨论的思想应用及方程的化简运算.

练习册系列答案
相关题目
7.函数f(x)=$\left\{\begin{array}{l}{\sqrt{2-|x-2|},}&{x∈[0,4]}\\{\frac{1}{2}f(x-4),}&{x∈(4,+∞)}\end{array}\right.$,若x>0时,不等式f(x)≤$\frac{m}{x}$恒成立,则实数m的取值范围为( )
| A. | [4$\sqrt{2}$,+∞) | B. | [3$\sqrt{2}$,+∞) | C. | [2$\sqrt{2}$,+∞) | D. | [$\frac{5}{2}$$\sqrt{2}$,+∞) |
4.某班级举行一次“科普知识”竞赛活动,活动分为初赛和决赛两个阶段.现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表:
(Ⅰ)填写频率分布表中的空格;
(Ⅱ)决赛规则如下:参加决赛的每位同学从给定的5道小题中依次口答,答对3道题就终止答题并获一等奖;如果前3道题都答错就不再答第4、5题而被淘汰.某同学进入决赛,每道题答对的概率均为0.5.
①求该同学恰好答满5道题并获一等奖的概率;
②记该同学决赛中答题的个数为X,求X的分布列及数学期望.
| 分 组(分数段) | 频 数(人 数) | 频 率 |
| [60,70) | 8 | |
| [70,80) | 0.44 | |
| [80,90) | 14 | 0.28 |
| [90,100 | ||
| 合 计 | 50 | 1 |
(Ⅱ)决赛规则如下:参加决赛的每位同学从给定的5道小题中依次口答,答对3道题就终止答题并获一等奖;如果前3道题都答错就不再答第4、5题而被淘汰.某同学进入决赛,每道题答对的概率均为0.5.
①求该同学恰好答满5道题并获一等奖的概率;
②记该同学决赛中答题的个数为X,求X的分布列及数学期望.
11.庄子说:“一尺之锤,日取其半.万世不竭”.这句话描述的问题实质是一个等比数列,设等比数列{an}的首项a1=1,前n项和Sn,则Sn一定满足( )
| A. | Sn>$\frac{3}{2}$ | B. | Sn<$\frac{3}{2}$ | C. | Sn>2 | D. | Sn<2 |