题目内容
4.某班级举行一次“科普知识”竞赛活动,活动分为初赛和决赛两个阶段.现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表:| 分 组(分数段) | 频 数(人 数) | 频 率 |
| [60,70) | 8 | |
| [70,80) | 0.44 | |
| [80,90) | 14 | 0.28 |
| [90,100 | ||
| 合 计 | 50 | 1 |
(Ⅱ)决赛规则如下:参加决赛的每位同学从给定的5道小题中依次口答,答对3道题就终止答题并获一等奖;如果前3道题都答错就不再答第4、5题而被淘汰.某同学进入决赛,每道题答对的概率均为0.5.
①求该同学恰好答满5道题并获一等奖的概率;
②记该同学决赛中答题的个数为X,求X的分布列及数学期望.
分析 (Ⅰ)由频率=$\frac{频数}{总数}$,能完成频率分布表.
(Ⅱ)①该同学答满5道题并获一等奖,即前4道题回答结果对错,而第5道题答对,由此能求出该同学恰好答满5道题并获一等奖的概率.
②该同学答题的个数可能为3、4、5,即X的可能取值为3、4、5,分另求出相应的概率,由此能求出X的分布列和数学期望.
解答 (本小题满分13分)
解:(Ⅰ)由频率=$\frac{频数}{总数}$,得频率分布表为:
| 分 组(分数段) | 频 数(人 数) | 频 率 |
| [60,70) | 8 | 0.16 |
| [70,80) | 22 | 0.44 |
| [80,90) | 14 | 0.28 |
| [90,100[来源:.Com | 6 | 0.12 |
| 合 计 | 50 | 1 |
(Ⅱ)①该同学答满5道题并获一等奖,即前4道题回答结果对错,而第5道题答对,
∴该同学恰好答满5道题并获一等奖的概率p=${C}_{4}^{2}(\frac{1}{2})^{2}(1-\frac{1}{2})^{2}•\frac{1}{2}$=$\frac{3}{16}$.(6分)
②该同学答题的个数可能为3、4、5,即X的可能取值为3、4、5,(7分)
X=3时分两种情况:答完3道题获奖或答完3道题淘汰,
P(X=3)=${C}_{3}^{3}(\frac{1}{2})^{3}$+${C}_{3}^{3}(1-\frac{1}{2})^{3}(\frac{1}{2})$=$\frac{1}{4}$,
X=4时分两种情况:答完4道题获奖或答完4道题淘汰,
P(X=4)=${C}_{3}^{2}(\frac{1}{2})^{2}•\frac{1}{2}•\frac{1}{2}$+${C}_{3}^{1}(\frac{1}{2})(\frac{1}{2})^{2}(\frac{1}{2})$=$\frac{3}{8}$,
X=5时分两种情况:答完5道题获奖或答完5道题淘汰,
P(X=5)=${C}_{4}^{2}(\frac{1}{2})^{2}(\frac{1}{2})^{2}(\frac{1}{2})$+${C}_{4}^{2}(\frac{1}{2})^{2}(\frac{1}{2})^{2}(1-\frac{1}{2})$=$\frac{3}{8}$,(10分)
∴X的分布列为:
| X | 3 | 4 | 5 |
| P | $\frac{1}{4}$ | $\frac{3}{8}$ | $\frac{3}{8}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意n次独立重复试验中事件A恰发生k次的概率计算公式的合理运用.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
14.复数z=$\frac{2-i}{i}$的共轭复数是( )
| A. | 2+i | B. | -2i-1 | C. | -1+2i | D. | 1-2i |
15.若圆${C_1}:{(x-1)^2}+{y^2}=1$与圆${C_2}:{x^2}+{y^2}-8x-8y+m=0$相交,则m的取值范围为( )
| A. | (-2,8) | B. | (-∞,-2)∪(8,+∞) | C. | (-4,16) | D. | (-∞,-4)∪(16,+∞) |
19.设Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5=( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
9.若复数z满足$\frac{z}{(1+i)^{2}}$=cos60°+isin60°,其中i为虚数单位,则z=( )
| A. | -$\sqrt{3}$-i | B. | -$\sqrt{3}$+i | C. | 1+$\sqrt{3}$i | D. | 1-$\sqrt{3}$i |
16.方程|x2-y|=1-|y|所表示的曲线是( )
| A. |  | B. | 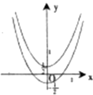 | C. |  | D. | 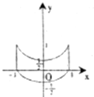 |
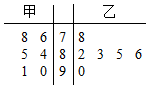 吉安市某校的甲乙两名同学在6次数学竞赛辅导测试中的成绩统计如图的茎叶图所示:
吉安市某校的甲乙两名同学在6次数学竞赛辅导测试中的成绩统计如图的茎叶图所示: