题目内容
11.庄子说:“一尺之锤,日取其半.万世不竭”.这句话描述的问题实质是一个等比数列,设等比数列{an}的首项a1=1,前n项和Sn,则Sn一定满足( )| A. | Sn>$\frac{3}{2}$ | B. | Sn<$\frac{3}{2}$ | C. | Sn>2 | D. | Sn<2 |
分析 由题意可得:a1=1,q=$\frac{1}{2}$,利用等比数列的前n项和公式即可得出.
解答 解:由题意可得:a1=1,q=$\frac{1}{2}$,
∴Sn=$\frac{1-(\frac{1}{2})^{n}}{1-\frac{1}{2}}$=$2[1-(\frac{1}{2})^{n}]$<2.
点评 本题考查了等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
1.中央电视台1套连续播放5个广告,其中3个不同的商业广告和2个不同的公益宣传广告,要求最后播放的必须是公益宣传广告,且2个公益宣传广告不能连续播放,则不同的播放方式有( )
| A. | 120种 | B. | 48种 | C. | 36种 | D. | 18种 |
2.设数列{an}是公差大于0的等差数列,且a8+a9+…+a12=0,则前n项和Sn最小时n的值为( )
| A. | 9 | B. | 10 | C. | 9或10 | D. | 19 |
19.设Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5=( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
6.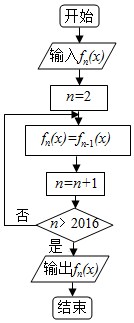 如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )
如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )
 如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )
如图程序框图中,当n∈N*(n>1)时,函数fn(x)表示函数fn-1(x)的导函数,即fn(x)=f′n-1(x).若输入函数f1(x)=sinx+cosx,则输出的函数fn(x)为( )| A. | $\sqrt{2}sin(x+\frac{π}{4})$ | B. | $-\sqrt{2}sin(x+\frac{π}{4})$ | C. | $\sqrt{2}sin(x-\frac{π}{4})$ | D. | $-\sqrt{2}sin(x-\frac{π}{4})$ |
16.方程|x2-y|=1-|y|所表示的曲线是( )
| A. |  | B. | 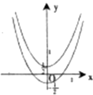 | C. |  | D. | 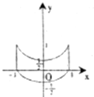 |
1.曲线f(x)=ln(2x-1)上的点到直线2x-y+3=0的最短距离是( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |