题目内容
7.函数f(x)=$\left\{\begin{array}{l}{\sqrt{2-|x-2|},}&{x∈[0,4]}\\{\frac{1}{2}f(x-4),}&{x∈(4,+∞)}\end{array}\right.$,若x>0时,不等式f(x)≤$\frac{m}{x}$恒成立,则实数m的取值范围为( )| A. | [4$\sqrt{2}$,+∞) | B. | [3$\sqrt{2}$,+∞) | C. | [2$\sqrt{2}$,+∞) | D. | [$\frac{5}{2}$$\sqrt{2}$,+∞) |
分析 利用函数与方程的关系求出函数f(x)的表达式,作出函数f(x)与g(x)=$\frac{m}{x}$的图象,利用数形结合建立不等式关系即可得到结论.
解答 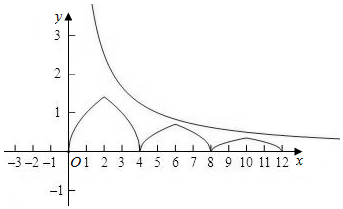 解:当0≤x≤4时,函数f(x)在[0,2]上为增函数,则[2,4]上为减函数,
解:当0≤x≤4时,函数f(x)在[0,2]上为增函数,则[2,4]上为减函数,
则当x=2时,函数f(x)取得最大值f(2)=$\sqrt{2}$,
当4≤x≤8时,0≤x-4≤4,
即f(x)=$\frac{1}{2}$f(x-4)=$\frac{1}{2}$$\sqrt{2-|x-6|}$,此时的最大值为f(6)=$\frac{\sqrt{2}}{2}$,
当8≤x≤12时,4≤x-4≤8,
即f(x)=$\frac{1}{2}$f(x-4)=$\frac{1}{4}$$\sqrt{2-|x-10|}$,此时的最大值为f(10)=$\frac{\sqrt{2}}{4}$,
作出函数f(x)的图象如图,要使当x>0时,不等式f(x)≤$\frac{m}{x}$恒成立,
则m>0,
设g(x)=$\frac{m}{x}$,
则满足$\left\{\begin{array}{l}{f(2)≤g(2)}\\{f(6)≤g(6)}\\{f(10)≤g(10)}\end{array}\right.$,即$\left\{\begin{array}{l}{\sqrt{2}≤\frac{m}{2}}\\{\frac{\sqrt{2}}{2}≤\frac{m}{6}}\\{\frac{\sqrt{2}}{4}≤\frac{m}{10}}\end{array}\right.$,即$\left\{\begin{array}{l}{m≥2\sqrt{2}}\\{m≥3\sqrt{2}}\\{m≥\frac{5\sqrt{2}}{2}}\end{array}\right.$,即m≥3$\sqrt{2}$,
故选:B.
点评 本题主要考查不等式恒成立问题,根据函数与不等式的关系,转化为两个函数的大小关系,利用数形结合是解决本题的关键.综合性较强,难度较大.

 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案| A. | (-∞,4] | B. | [4,+∞) | C. | [-4,4] | D. | (-4,4] |
| A. | (-2,8) | B. | (-∞,-2)∪(8,+∞) | C. | (-4,16) | D. | (-∞,-4)∪(16,+∞) |
| A. | 9 | B. | 10 | C. | 9或10 | D. | 19 |
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
| A. |  | B. |  | C. |  | D. |  |
| A. | [1-π,1] | B. | [0,2] | C. | (-∞,1] | D. | [-1,1] |
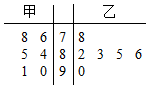 吉安市某校的甲乙两名同学在6次数学竞赛辅导测试中的成绩统计如图的茎叶图所示:
吉安市某校的甲乙两名同学在6次数学竞赛辅导测试中的成绩统计如图的茎叶图所示: