题目内容

6．设命题甲：关于x的不等式x2+2ax+4≤0有解，命题乙：设函数f（x）=loga（x+a-2）在区间（1，+∞）上恒为正值，那么甲是乙的必要不充分条件．

分析 命题甲：关于x的不等式x2+2ax+4≤0有解，可得△≥0．命题乙：设函数f（x）=loga（x+a-2）在区间（1，+∞）上恒为正值，则$\left\{\begin{array}{l}{a＞1}\\{lo{g}_{a}（x+a-2）≥f（1）=0}\end{array}\right.$，解得a即可判断出结论．

解答 解：命题甲：关于x的不等式x2+2ax+4≤0有解，
∴△=4a2-16≥0，解得a≥2或a≤-2．
命题乙：设函数f（x）=loga（x+a-2）在区间（1，+∞）上恒为正值，
∴$\left\{\begin{array}{l}{a＞1}\\{lo{g}_{a}（x+a-2）≥f（1）=0}\end{array}\right.$，解得a≥2．
那么甲是乙的必要不充分．
故答案为：必要不充分．

点评 本题考查了不等式的解法、函数的性质、简易逻辑的判定方法，考查了计算能力，属于中档题．

练习册系列答案
相关题目
16．下列说法正确的有（　　）
（1）如果两个平面有三个公共点，则这两个平面重合．
（2）m，n为异面直线，过空间任意一点P，一定能作一条直线l与m，n都垂直
（3）m，n为异面直线，过空间任意一点P，一定能作一条直线l与m，n都相交
（4）m，n为异面直线，过空间任意一点P，一定存在与直线m，n都平行的平面．
A．1个B．2个C．3个D．4个
17．已知函数f（x）=logsin1（x2-ax+3a）在[2，+∞）单调递减，则实数a的取值范围是（　　）
A．（-∞，4]B．[4，+∞）C．[-4，4]D．（-4，4]
14．复数z=$\frac{2-i}{i}$的共轭复数是（　　）
A．2+iB．-2i-1C．-1+2iD．1-2i
1．中央电视台1套连续播放5个广告，其中3个不同的商业广告和2个不同的公益宣传广告，要求最后播放的必须是公益宣传广告，且2个公益宣传广告不能连续播放，则不同的播放方式有（　　）
A．120种B．48种C．36种D．18种
11．下列四种说法：
①命题“?x∈R，都有x2-2＜3x”的否定是“?x∈R，使得x2-2≥3x”；
②若a，b∈R，则2a＜2b是log${\;}_{\frac{1}{2}}$a＞log${\;}_{\frac{1}{2}}$b的必要不充分条件；
③把函数y=sin（-3x）（x∈R）的图象上所有的点向右平移$\frac{π}{4}$个单位即可得到函数y=sin（-3x-$\frac{π}{4}$）（x∈R）的图象；
④若向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=2，且$\overrightarrow{a}$与b的夹角为$\frac{2π}{3}$，则|$\overrightarrow{a}$+$\overrightarrow{b}$|=$\sqrt{3}$．
其中正确的说法是①②④．
18．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;（a＞b＞0）$的离心率为$\frac{{\sqrt{2}}}{2}$，且椭圆上点到椭圆C左焦点F1距离的最小值为$\sqrt{2}-1$．
（1）求C的方程；
（2）若B2为上顶点，F2为右焦点，则求∠B2F1F2的度数．
15．若圆${C_1}：{（x-1）^2}+{y^2}=1$与圆${C_2}：{x^2}+{y^2}-8x-8y+m=0$相交，则m的取值范围为（　　）
A．（-2，8）B．（-∞，-2）∪（8，+∞）C．（-4，16）D．（-∞，-4）∪（16，+∞）
16．方程|x2-y|=1-|y|所表示的曲线是（　　）
A．B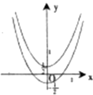．C．D．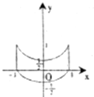

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网