题目内容
8.设函数f(x)=x2+ax+b,a,b∈R.(1)若a+b=3,当x∈[1,2]时,f(x)≥0恒成立,求实数a的取值范围;
(2)是否存在实数对(a,b),使得不等式|f(x)|>2在区间[1,5]上无解,若存在,试求出所有满足条件的实数对(a,b);若不存在,请说明理由.
分析 (1)分离参数得到$a≥-\frac{{{x^2}+3}}{x-1}$,结合基本不等式的性质得到a的范围即可;
(2)根据二次函数的性质得到关于a的不等式组,解出即可.
解答 解:(1)由f(x)≥0,即a(x-1)≥-(x2+3).
当x=1时,恒成立;
当x∈(1,2]时,得$a≥-\frac{{{x^2}+3}}{x-1}$,
令t=x-1∈(0,1],
$-\frac{{{x^2}+3}}{x-1}=-({t+\frac{4}{t}})-2$≤-7
综上:有a≥-7.
(2)要使|f(x)|>2在区间[1,5]上无解,
必须满足$\left\{\begin{array}{l}-2≤f(1)≤2\\-2≤f(3)≤2\\-2≤f(5)≤2\end{array}\right.$,
即 $\left\{\begin{array}{l}-2≤1+a+b≤2①\\-2≤9+3a+b≤2②\\-2≤25+5a+b≤2③\end{array}\right.$
由$\left\{\begin{array}{l}-2≤-1-a-b≤2①\\-2≤9+3a+b≤2②\end{array}\right.$,
相加得:-4≤8+2a≤4⇒-6≤a≤2
再由$\left\{\begin{array}{l}-2≤-9-3a-b≤2②\\-2≤25+5a+b≤2③\end{array}\right.$,
相加得:-4≤16+2a≤4⇒-10≤a≤-6
可以解得:a=-6,代入不等式组,得到b=7.
检验a=-6,时,|f(x)|≤2在区间[1,5]上恒成立
所以满足题意的是实数对(a,b)只有一对:(-6,7).
点评 本题考查了二次函数的性质,考查不等式的性质,是一道中档题.

练习册系列答案
相关题目
19.设Sn是等差数列{an}的前n项和,若a1+a3+a5=3,则S5=( )
| A. | 5 | B. | 7 | C. | 9 | D. | 11 |
16.方程|x2-y|=1-|y|所表示的曲线是( )
| A. |  | B. | 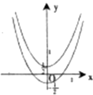 | C. |  | D. | 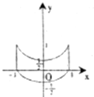 |
17.使arccos(1-x)有意义的x的取值范围是( )
| A. | [1-π,1] | B. | [0,2] | C. | (-∞,1] | D. | [-1,1] |