题目内容
6.已知函数f(x)=ax2+bx+c(a>0),满足f(1-x)=f(1+x),则f(2013x)与f(2014x)的大小关系是f(2013x)≤f(2014x).分析 函数f(x)的图象是开口朝上,且以直线x=1为对称轴的抛物线,结合指数函数的图象和性质,分类讨论可得答案.
解答 解:∵函数f(x)=ax2+bx+c(a>0),且f(1-x)=f(1+x),
故函数f(x)的图象是开口朝上,且以直线x=1为对称轴的抛物线,
当x<0时,1>2013x>2014x>0,此时f(2013x)<f(2014x),
当x=0时,2013x=2014x=1,此时f(2013x)=f(2014x),
当x>0时,1<2013x<2014x,此时f(2013x)<f(2014x),
综上可得:f(2013x)≤f(2014x),
故答案为:f(2013x)≤f(2014x).
点评 本题考查的知识点是二次函数的图象和性质,指数函数的图象和性质,难度中档.

练习册系列答案
相关题目
16.方程|x2-y|=1-|y|所表示的曲线是( )
| A. |  | B. | 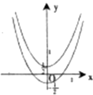 | C. |  | D. | 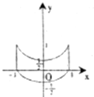 |
17.使arccos(1-x)有意义的x的取值范围是( )
| A. | [1-π,1] | B. | [0,2] | C. | (-∞,1] | D. | [-1,1] |
1.曲线f(x)=ln(2x-1)上的点到直线2x-y+3=0的最短距离是( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 3 |
 如图,AB是圆的直径,C是圆上的点,且PA⊥BC.
如图,AB是圆的直径,C是圆上的点,且PA⊥BC.