题目内容
已知直线l:x-2y+8=0和两点A(2,0),B(-2,-4),若直线l上存在点P使得|PA|+|PB|最小,则点P的坐标为 .
考点:两点间距离公式的应用
专题:直线与圆
分析:先判断A、B与直线l:x+2y-2=0的位置关系,即把点的坐标代入x+2y-2,看符号相同在同侧,相反异侧.使|PA|+|PB|最小,如果A、B在l的同侧,将其中一点对称到l的另一侧,连线与l的交点即为P;如果A、B在l的异侧,则直接连线求交点P即可.
解答:
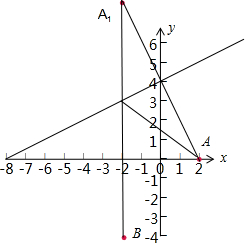 解:可判断A、B在直线l的同侧,设A点关于l的对称点A1的坐标为(x1,y1).
解:可判断A、B在直线l的同侧,设A点关于l的对称点A1的坐标为(x1,y1).
则有
-2•
+8=0,
•
=-1.
解得:x1=-2,y1=8.
直线A1B的方程为x=-2,直线A1B与l的交点可求得为P(-2,3).
由平面几何知识可知|PA|+|PB|最小.
故答案为:(-2,3).
 解:可判断A、B在直线l的同侧,设A点关于l的对称点A1的坐标为(x1,y1).
解:可判断A、B在直线l的同侧,设A点关于l的对称点A1的坐标为(x1,y1).则有
| x1+2 |
| 2 |
| y1 |
| 2 |
| y1 |
| x1-2 |
| 1 |
| 2 |
解得:x1=-2,y1=8.
直线A1B的方程为x=-2,直线A1B与l的交点可求得为P(-2,3).
由平面几何知识可知|PA|+|PB|最小.
故答案为:(-2,3).
点评:本题考查点与直线的位置关系,直线关于直线对称问题,以及平面几何知识,是中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
已知点P(x,y)的坐标满足条件
,O为坐标原点,则直线OP的斜率取值范围是( )
|
| A、[3,5] |
| B、[2,5] |
| C、(-∞,3]∪[5,+∞) |
| D、(-∞,2]∪[5,+∞) |
 二次函数f(x)=ax2+bx+c的导函数y=f′(x)的图象如图所示,且f(x)的极大值为4,则f(3)=( )
二次函数f(x)=ax2+bx+c的导函数y=f′(x)的图象如图所示,且f(x)的极大值为4,则f(3)=( )| A、16 | B、-2 | C、0 | D、8 |
已知a>1,-1<b<0,那么( )
| A、ab>b |
| B、ab<-a |
| C、ab2<ab |
| D、ab2>b2 |