题目内容
解不等式:
(1)log(2x-3)(x2-3)>0;
(2)-4<-
x2-x-
<-2.
(1)log(2x-3)(x2-3)>0;
(2)-4<-
| 1 |
| 2 |
| 3 |
| 2 |
考点:指、对数不等式的解法,一元二次不等式的解法
专题:不等式的解法及应用
分析:(1)利用对数的运算性质,对底数2x-3分0<2x-3<1与2x-3>1讨论,解相应的不等式,最后取并即可;
(2)利用一元二次不等式的解法分别解-
x2-x-
>-4与-
x2-x-
<-2,最后取交集即可.
(2)利用一元二次不等式的解法分别解-
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:(1)当0<2x-3<1,即
<x<2时,由原不等式得:
,解得
<x<2或-2<x<-
(舍去),
∴
<x<2;
当2x-3>1,即x>2时,同理可得x>2;
综上所述,不等式log(2x-3)(x2-3)>0的解集为{x|
<x<2或x>2};
(2)由-
x2-x-
>-4得x2+2x-5<0,解得:-1-
<x<-1+
;①
由-
x2-x-
<-2得:x2+2x-1>0,解得:x<-1-
或x>-1+
;②
由①②得:-1-
<x<-1-
或-1+
<x<-1+
;
∴原不等式的解集为{x|-1-
<x<-1-
或-1+
<x<-1+
}.
| 3 |
| 2 |
|
| 3 |
| 3 |
∴
| 3 |
当2x-3>1,即x>2时,同理可得x>2;
综上所述,不等式log(2x-3)(x2-3)>0的解集为{x|
| 3 |
(2)由-
| 1 |
| 2 |
| 3 |
| 2 |
| 6 |
| 6 |
由-
| 1 |
| 2 |
| 3 |
| 2 |
| 2 |
| 2 |
由①②得:-1-
| 6 |
| 2 |
| 2 |
| 6 |
∴原不等式的解集为{x|-1-
| 6 |
| 2 |
| 2 |
| 6 |
点评:本题考查对数不等式的解法与一元二次不等式的解法,考查运算求解能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
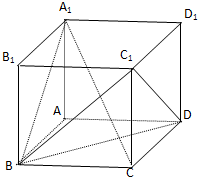 如图,正方体ABCD-A1B1C1D1的棱长为1.
如图,正方体ABCD-A1B1C1D1的棱长为1.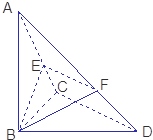 已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且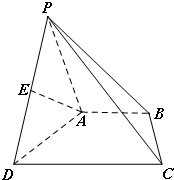 如图,在四棱锥P-ABCD中,BA⊥平面PAD,AP=AD,DC∥AB,DC=2AB,E是棱
如图,在四棱锥P-ABCD中,BA⊥平面PAD,AP=AD,DC∥AB,DC=2AB,E是棱