题目内容
已知侧棱长为a的正三棱锥P-ABC的侧面都是直角三角形,且四个顶点都在一个球面上,则该球的表面积为 .
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:侧棱长为a的正三棱锥P-ABC的侧面都是直角三角形,且四个顶点都在一个球面上,说明三棱锥的正方体的一个角,把三棱锥扩展为正方体,它们有相同的外接球,球的直径就是正方体的对角线,求出直径,即可求出球的表面积.
解答:
解:因为侧棱长为a的正三棱锥P-ABC的侧面都是直角三角形,且四个顶点都在一个球面上,
三棱锥的正方体的一个角,把三棱锥扩展为正方体,它们有相同的外接球,
球的直径就是正方体的对角线,正方体的对角线长为:
a;
所以球的表面积为:4π(
)2=3πa2
故答案为:3πa2.
三棱锥的正方体的一个角,把三棱锥扩展为正方体,它们有相同的外接球,
球的直径就是正方体的对角线,正方体的对角线长为:
| 3 |
所以球的表面积为:4π(
| ||
| 2 |
故答案为:3πa2.
点评:本题是基础题,考查三棱锥的外接球的表面积的求法,三棱锥扩展为正方体是本题的关键,正方体的对角线是外接球的直径也不容忽视,考查计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
有6本不同的书,分成四份,每份至少一本,则不同的方法有( )
| A、110 | B、45 |
| C、65 | D、165 |
已知条件p:log2(x-1)<1;条件q:|x-2|<1,则p是q成立的( )
| A、充分必要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分又不必要条件 |
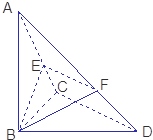 已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且
已知△BCD中,∠BCD=90°,BC=CD=a,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且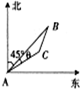 海中有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°方向上且与点A相距40
海中有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°方向上且与点A相距40