题目内容
已知a>1,-1<b<0,那么( )
| A、ab>b |
| B、ab<-a |
| C、ab2<ab |
| D、ab2>b2 |
考点:不等式比较大小
专题:不等式的解法及应用
分析:两边同乘以一个正数和负数,利用不等式的性质,判断即可.
解答:
解:∵a>1,-1<b<0
∴ab<b,ab>-a,ab2>ab,ab2>b2,
故A,B,C错误,D正确,
故选:D.
∴ab<b,ab>-a,ab2>ab,ab2>b2,
故A,B,C错误,D正确,
故选:D.
点评:本题主要考查了不等式的性质,两边同乘以的数是正数还是负数是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
在极坐标系中,点(2,
)到圆ρ=4cosθ的圆心的距离为( )
| π |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
已知条件p:log2(x-1)<1;条件q:|x-2|<1,则p是q成立的( )
| A、充分必要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分又不必要条件 |
若不等式|x+a|<6的解集为(-1,11),则实数a等于( )
| A、-1 | B、-7 | C、7 | D、-5 |
若两条直线y=a2x-1与y=(a+2)x-a+1互相平行,则a等于( )
| A、2 | B、1 | C、-2 | D、-1 |
已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则A∪B=( )
| A、{2} |
| B、{2,3,4} |
| C、{1,2,3,4} |
| D、{0,2,3,4} |
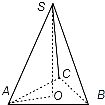 如图,在三棱锥S-ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为( )
如图,在三棱锥S-ABC中,底面是边长为1的等边三角形,侧棱长均为2,SO⊥底面ABC,O为垂足,则侧棱SA与底面ABC所成角的余弦值为( )