题目内容
已知函数f(x)=
在区间[-1,m]上的最大值是2,则m的取值范围是 .
|
考点:分段函数的应用
专题:函数的性质及应用
分析:可以利用函数的图象,观察即可,或分别利用函数的单调性,求出最大值是2的自变量的范围,继而得到m的范围.
解答:
解:法一,画出函数f(x)的图象,如图所示,
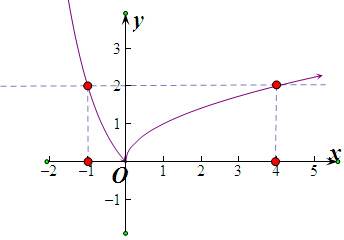
在区间[-1,m]上的最大值是2,由图象可知,m的取值范围是(-1,4].
法二,因为f(x)=3-x-1在(-∞,0]为减函数,所以3-x-1≥2,解得-1≤x≤0,
因为f(x)=x
在(0,+∞)为增函数,所以x
-1≤2,解得0<x≤4,
所以当x在[-1,4]上的最大值为2,
故m的取值范围是(-1,4].
故答案为:(-1,4].

在区间[-1,m]上的最大值是2,由图象可知,m的取值范围是(-1,4].
法二,因为f(x)=3-x-1在(-∞,0]为减函数,所以3-x-1≥2,解得-1≤x≤0,
因为f(x)=x
| 1 |
| 2 |
| 1 |
| 2 |
所以当x在[-1,4]上的最大值为2,
故m的取值范围是(-1,4].
故答案为:(-1,4].
点评:本题主要考查了函数的分段函数问题,本题的关键是判断出函数的单调区间,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在极坐标系中,点(2,
)到圆ρ=4cosθ的圆心的距离为( )
| π |
| 3 |
| A、2 | ||||
B、
| ||||
C、
| ||||
D、
|
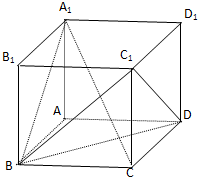 如图,正方体ABCD-A1B1C1D1的棱长为1.
如图,正方体ABCD-A1B1C1D1的棱长为1.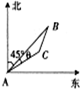 海中有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°方向上且与点A相距40
海中有一个雷达观测站A,某时刻测得一艘匀速直线行驶的船只位于点A北偏东45°方向上且与点A相距40