题目内容
设函数f(x)=x2-(a-2)x-alnx,若f(x)在[1,2]上的最小值为1,求实数a的值.
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:先求导,再分类讨论,根据函数的单调性求出a的值.
解答:
解:∵f(x)=x2-(a-2)x-alnx,
∴f′(x)=2x-(a-2)-
=
,
当
≥2,即a≥4时,f(x)单调递减,f(x)min=f(2)=4-2(a-2)-aln2=1,解得a=-
<0(舍去)
当1<
<2时,即2<a<4时,f(x)在[1,
]单调递增,在(
,2]单调递减,f(x)min=f(
)=-
+a-aln
<0≠1,
当
≤1时,即a≤2时,f(x)单调递增,f(x)min=f(1)=3-a=1,
解得a=2,
综上所述a的值为2.
∴f′(x)=2x-(a-2)-
| a |
| x |
| (x+1)(2x-a) |
| x |
当
| a |
| 2 |
| 1 |
| 2+ln2 |
当1<
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| a2 |
| 4 |
| a |
| 2 |
当
| a |
| 2 |
解得a=2,
综上所述a的值为2.
点评:本题主要考查了利用导数研究函数的单调性,以及利用导数求闭区间上函数的最值,属于中档题.

练习册系列答案
相关题目
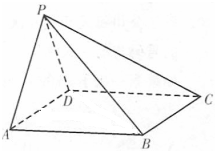 四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,点P为平面ABCD所在平面外的一点,若△PAD为等边三角形,求证:PB⊥AD.
四棱锥P-ABCD中,底面ABCD为菱形,且∠DAB=60°,点P为平面ABCD所在平面外的一点,若△PAD为等边三角形,求证:PB⊥AD.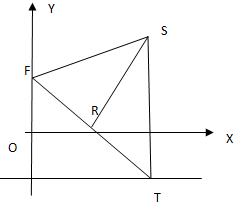 在平面直角坐标系中,O为坐标原点,点 F,T,R,S满足
在平面直角坐标系中,O为坐标原点,点 F,T,R,S满足