题目内容
若两个平面法向量分别是
=(1,0,1),
=(-1,1,0),则这两个平面所成的锐二面角的大小是 .
| a |
| b |
考点:二面角的平面角及求法
专题:空间角
分析:直接利用空间向量的数量积求解两个平面的二面角的大小即可.
解答:
解:两个平面法向量分别是
=(1,0,1),
=(-1,1,0),
则这两个平面所成的二面角的大小是θ.
cosθ=
=
=-
.
这两个平面所成的锐二面角的大小是:
.
故答案为:
.
| a |
| b |
则这两个平面所成的二面角的大小是θ.
cosθ=
| ||||
|
|
| -1 | ||||
|
| 1 |
| 2 |
这两个平面所成的锐二面角的大小是:
| π |
| 3 |
故答案为:
| π |
| 3 |
点评:本题考查二面角的大小的求法,空间向量的数量积的应用,考查计算能力.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
某学校联欢会安排有小品、相声、朗诵、唱歌、舞蹈五个节目.要求小品播在舞蹈之前,并且这两个节目不能相邻,则节目表不同的排法种数为( )
| A、24 | B、36 | C、72 | D、84 |
集合A={x|
≤0},B={y|y=ln(x-1)},则A∩B等于( )
| x |
| x-1 |
| A、[0,1) | B、∅ |
| C、(0,1) | D、[0,1] |
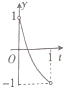
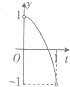
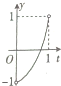
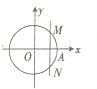 在如图所示的直角坐标系中,点A为圆O:x2+y2=1与x轴的交点,垂直于x轴的动直线l从点A出发,以1m/s的速度沿x轴向左移动,记直线l与圆O的交点为M,N,劣弧MN的长为x,令y=cosx,则y与时间t(0<t<1,单位:s)的函数y=f(x)的图象大致为( )
在如图所示的直角坐标系中,点A为圆O:x2+y2=1与x轴的交点,垂直于x轴的动直线l从点A出发,以1m/s的速度沿x轴向左移动,记直线l与圆O的交点为M,N,劣弧MN的长为x,令y=cosx,则y与时间t(0<t<1,单位:s)的函数y=f(x)的图象大致为( )