直线mx+(1-m)y+m-2=0一定过定点．题目和参考答案——青夏教育精英家教网—

题目内容

直线mx+（1-m）y+m-2=0一定过定点

．

考点：恒过定点的直线

专题：计算题,直线与圆

分析：直线mx+（1-m）y+m-2=0可化为y-2+m（x-y+1）=0，根据x=1，y=2时方程恒成立，可直线过定点的坐标．

解答： 解：直线mx+（1-m）y+m-2=0可化为y-2+m（x-y+1）=0，
∴

y-2=0

x-y+1=0

，
∴x=1，y=2，
∴直线mx+（1-m）y+m-2=0过定点（1，2）．
故答案为：（1，2）．

点评：本题考查的知识点是恒过定义的直线，解答的关键是将参数分离，化为Am+B=0的形式（其中m为参数），令A，B=0可得答案．

练习册系列答案

新课程寒假作业本山西教育出版社系列答案

相关题目

某程序图如图所示，该程序运行后输出的结果是（　　）

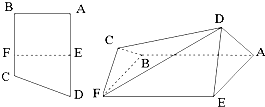如图：直角梯形ABCD中，AD∥BC，∠ABC=90°，E，F分别为边AD和BC上的点，且EF∥AB，AD=2AE=2AB=4FC=4，将四边形EFCD沿EF折起成如图的位置，使AD=AE．
（Ⅰ）求证：BC∥平面DAE；
（Ⅱ）求四棱锥D-AEFB的体积；
（Ⅲ）求面CBD与面DAE所成锐二面角的余弦值．

下列四种说法中，
①命题“存在x∈R，x²-x＞0”的否定是“对于任意x∈R，x²-x＜0”；
②命题“p且q为真”是“p或q为真”的必要不充分条件；
③已知幂函数f（x）=x^α的图象经过点(2，

+y²=1的左、右焦点分别为F₁，F₂，
（Ⅰ）当直线l过F₂时，求m的值；
（Ⅱ）设直线l与椭圆C交于A，B两点，△AF₁F₂、△BF₁F₂的重心分别为G、H，若原点在以线段GH为直径的圆内，求实数m的取值范围．

已知直线m，n和平面α，满足m?α，n∥α，则直线m，n的关系是（　　）

A、平行	B、相交
C、异面	D、平行或异面

已知线段AB的端点B在圆C₁：x²+（y-4）²=16上运动，端点A的坐标为（4，0），线段AB中点为M，
（Ⅰ）试求M点的轨C₂方程；
（Ⅱ）若圆C₁与曲线C₂交于C，D两点，试求线段CD的长．

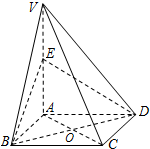如图，在四棱锥V-ABCD中，底面ABCD是正方形，侧棱VA⊥底面ABCD，点E为VA的中点．
（Ⅰ）求证：VC∥平面BED；
（Ⅱ）求证：平面VAC⊥平面BED．

在关于x的方程x²-ax+4=0，x²+（a-1）x+16=0，x²+2ax+3a+10=0中，已知至少有一个方程有实数根，则实数a的取值范围为（　　）

试题分类