题目内容
已知直线m，n和平面α，满足m?α，n∥α，则直线m，n的关系是（ ）
| A、平行 | B、相交 |
| C、异面 | D、平行或异面 |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：根据直线与平面的位置关系，m?α，n∥α，得到m，n一定没有公共点，因此它们平行或者异面．
解答：
解：因为m?α，n∥α，
所以直线m，n没有公共点，
所以直线m，n平行或者异面．
故选D．
所以直线m，n没有公共点，
所以直线m，n平行或者异面．
故选D．
点评：本题考查了直线与直线、直线与平面的位置关系的判断，属于基础题．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
下列判断，正确的是（ ）
| A、平行于同一平面的两直线平行 |
| B、垂直于同一直线的两直线平行 |
| C、垂直于同一平面的两平面平行 |
| D、垂直于同一平面的两直线平行 |
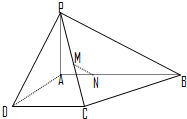如图所示，在四棱锥P-ABCD中，AB⊥AD，AD⊥DC，PA⊥底面ABCD，PA=AD=DC=过点P（-1，4）作圆x2+y2-4x-6y+12=0的切线，则切线长为（ ）
| A、3 | ||
B、
| ||
C、
| ||
| D、5 |