题目内容
下列四种说法中,
①命题“存在x∈R,x2-x>0”的否定是“对于任意x∈R,x2-x<0”;
②命题“p且q为真”是“p或q为真”的必要不充分条件;
③已知幂函数f(x)=xα的图象经过点(2,
),则f(4)的值等于
;
④已知向量
=(3,-4),
=(2,1),则向量
在向量
方向上的投影是
.
说法正确的个数是( )
①命题“存在x∈R,x2-x>0”的否定是“对于任意x∈R,x2-x<0”;
②命题“p且q为真”是“p或q为真”的必要不充分条件;
③已知幂函数f(x)=xα的图象经过点(2,
| ||
| 2 |
| 1 |
| 2 |
④已知向量
| a |
| b |
| a |
| b |
| 2 |
| 5 |
说法正确的个数是( )
| A、1 | B、2 | C、3 | D、4 |
考点:命题的真假判断与应用
专题:简易逻辑
分析:本题①根据命题否定的规律判断命题是否为真;②化简研究命题中的条件和结论,从而判断条件间的关系;③根据函数图象上的点坐标,得到参数a的值,再利用解析式求出函数的值;④利用平面向量的数量积与投影的关系,判断命题是否正确,得到本题结论.
解答:
解:①命题“存在x∈R,x2-x>0”的否定是“对于任意x∈R,x2-x≤0”,
故命题①不正确;
②命题“p且q为真”,则命题p、q均为真,
∴“p或q为真”.
反之“p或q为真”,则p、q不一定都真,
∴不一定有“p且q为真”,
∴命题“p且q为真”是“p或q为真”的充分不必要条件,
故命题②不正确;
③由幂函数f(x)=xα的图象经过点(2,
),
∴2α=
,
∴α=-
,
∴幂函数为f(x)=x-
,
∴f(4)=4-
=
,
∴命题③正确;
④向量
在向量
方向上的投影是|
|cosθ=
=
=
,
其中θ是
和
的夹角,
故④错误.
∴正确的命题有一个.
故选A.
故命题①不正确;
②命题“p且q为真”,则命题p、q均为真,
∴“p或q为真”.
反之“p或q为真”,则p、q不一定都真,
∴不一定有“p且q为真”,
∴命题“p且q为真”是“p或q为真”的充分不必要条件,
故命题②不正确;
③由幂函数f(x)=xα的图象经过点(2,
| ||
| 2 |
∴2α=
| ||
| 2 |
∴α=-
| 1 |
| 2 |
∴幂函数为f(x)=x-
| 1 |
| 2 |
∴f(4)=4-
| 1 |
| 2 |
| 1 |
| 2 |
∴命题③正确;
④向量
| a |
| b |
| a |
| ||||
|
|
| 2 | ||
|
2
| ||
| 5 |
其中θ是
| a |
| b |
故④错误.
∴正确的命题有一个.
故选A.
点评:本题考查了命题真假的判断,还考查了命题的否定、充要条件、幂函数解析式和向量的投影等知识,本题难度不大,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若α,β,γ表示平面,m,n表示直线,则下列命题中,正确的是( )
| A、m?α,n?α,m∥β,n∥β,则α∥β |
| B、若α⊥γ,β⊥γ,则α∥β |
| C、若α∥β,m?α,n?β,则m∥n |
| D、若α∥β,m?α,则m∥β |
下列判断,正确的是( )
| A、平行于同一平面的两直线平行 |
| B、垂直于同一直线的两直线平行 |
| C、垂直于同一平面的两平面平行 |
| D、垂直于同一平面的两直线平行 |
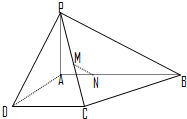 如图所示,在四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=DC=
如图所示,在四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=DC=