题目内容
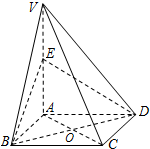 如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧棱VA⊥底面ABCD,点E为VA的中点.
如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧棱VA⊥底面ABCD,点E为VA的中点.(Ⅰ)求证:VC∥平面BED;
(Ⅱ)求证:平面VAC⊥平面BED.
考点:直线与平面平行的判定,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(Ⅰ)连结OE,证明:OE∥VC,利用线面平行的判定定理证明VC∥平面BED;
(Ⅱ)证明BD⊥平面VAC,利用平面与平面垂直的判定定理证明平面VAC⊥平面BED.
(Ⅱ)证明BD⊥平面VAC,利用平面与平面垂直的判定定理证明平面VAC⊥平面BED.
解答:
证明:(Ⅰ)连结OE.
∵底面ABCD是正方形,∴O为AC的中点.
又E为VA的中点,∴OE∥VC.…(3分)
又VC?平面BED,OE?平面BED,
∴VC∥平面BED.…(6分)
(Ⅱ)∵VA⊥平面ABCD,∴VA⊥BD.…(7分)
又 AC⊥BD,AC∩VA=A,
∴BD⊥平面VAC.…(10分)
∵BD?平面BED,
∴平面VAC⊥平面BED.…(12分)
∵底面ABCD是正方形,∴O为AC的中点.
又E为VA的中点,∴OE∥VC.…(3分)
又VC?平面BED,OE?平面BED,
∴VC∥平面BED.…(6分)
(Ⅱ)∵VA⊥平面ABCD,∴VA⊥BD.…(7分)
又 AC⊥BD,AC∩VA=A,
∴BD⊥平面VAC.…(10分)
∵BD?平面BED,
∴平面VAC⊥平面BED.…(12分)
点评:本题考查线面平行的判定定理、考查平面与平面垂直的判定定理,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若α,β,γ表示平面,m,n表示直线,则下列命题中,正确的是( )
| A、m?α,n?α,m∥β,n∥β,则α∥β |
| B、若α⊥γ,β⊥γ,则α∥β |
| C、若α∥β,m?α,n?β,则m∥n |
| D、若α∥β,m?α,则m∥β |
过点P(-1,4)作圆x2+y2-4x-6y+12=0的切线,则切线长为( )
| A、3 | ||
B、
| ||
C、
| ||
| D、5 |
圆x2+y2-4x=0和圆x2+y2+2y=0的位置关系是( )
| A、相离 | B、外切 | C、相交 | D、内切 |
 如图所示,在四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=DC=
如图所示,在四棱锥P-ABCD中,AB⊥AD,AD⊥DC,PA⊥底面ABCD,PA=AD=DC= 三棱锥P-ABC中,已知PC=10,AB=8,E、F分别为PA、BC的中点,EF=
三棱锥P-ABC中,已知PC=10,AB=8,E、F分别为PA、BC的中点,EF=