题目内容
已知点M(1,1,1),N(0,a,0),O(0,0,0),若△OMN为直角三角形,则a= .
考点:向量的数量积判断向量的共线与垂直
专题:平面向量及应用
分析:求出
=(-1,a-1,-1),
=(1,1,1),
=(0,a,0),运用数量积为零求解,注意特殊情况.
| MN |
| OM |
| 0N |
解答:
解:∵点M(1,1,1),N(0,a,0),O(0,0,0),
∴
=(-1,a-1,-1),
=(1,1,1),
=(0,a,0),
∵△OMN为直角三角形,
∴
•
=0,或),
•
=0,或
•
=0
即a-3=0,a=0,a(a-1)=0,
∵M,N不重合
∴a=3或a=1,a=0(舍去)
故答案为:3或1
∴
| MN |
| OM |
| 0N |
∵△OMN为直角三角形,
∴
| MN |
| OM |
| OM |
| 0N |
| MN |
| 0N |
即a-3=0,a=0,a(a-1)=0,
∵M,N不重合
∴a=3或a=1,a=0(舍去)
故答案为:3或1
点评:本题考查了向量的应用判断垂直问题,难度不大,

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
已知集合A={x|x2-3x-3≥0},B={x|-2≤x≤2},则A∩B=( )
| A、[-2,-1] |
| B、[-1,-1] |
| C、[-1,2) |
| D、[1,2) |
记数列{an}的前n项和为Sn,若不等式an2+
≥ma12对任意等差数列{an}及任意正整数n都成立,则实数m的最大值为( )
| Sn2 |
| n2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
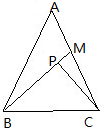 如图,在△ABC中,AB=AC=3
如图,在△ABC中,AB=AC=3