题目内容
德国著名数学家狄利克雷在数学领域成就显著,以其名命名的函数f(x)=
被称为狄利克雷函数,其中R为实数集,Q为有理数集,则关于函数有如下四个命题:
①f(f(x))=0;
②函数f(x)是偶函数;
③任取一个不为零的有理数T,f(x+T)=f(x)对任意的x∈R恒成立;
④存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3)),使得△ABC为等边三角形.
其中的真命题是( )
|
①f(f(x))=0;
②函数f(x)是偶函数;
③任取一个不为零的有理数T,f(x+T)=f(x)对任意的x∈R恒成立;
④存在三个点A(x1,f(x1)),B(x2,f(x2)),C(x3,f(x3)),使得△ABC为等边三角形.
其中的真命题是( )
| A、①②④ | B、②③ |
| C、③④ | D、②③④ |
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:①,根据函数的对应法则,可得不管x是有理数还是无理数,均有f(f(x))=1,从而可判断①;
②,根据函数奇偶性的定义,可得f(x)是偶函数,可判断②;
③,根据函数的表达式,结合有理数和无理数的性质,得f(x+T)=f(x),可判断③;
对于④,取x1=-
,x2=0,x3=
,可得A(-
,0)、B(0,1)、C(
,0)三点恰好构成等边三角形,可判断④.
②,根据函数奇偶性的定义,可得f(x)是偶函数,可判断②;
③,根据函数的表达式,结合有理数和无理数的性质,得f(x+T)=f(x),可判断③;
对于④,取x1=-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
解答:
解:对于①,∵当x为有理数时,f(x)=1;当x为无理数时,f(x)=0,
∴当x为有理数时,f(f(x))=f(1)=1;当x为无理数时,f(f(x))=f(0)=1,
即不管x是有理数还是无理数,均有f(f(x))=1,故①错误;
对于②,因为有理数的相反数还是有理数,无理数的相反数还是无理数,
所以对任意x∈R,都有f(-x)=f(x),故②正确;
对于③,若x是有理数,则x+T也是有理数; 若x是无理数,则x+T也是无理数,
∴根据函数的表达式,任取一个不为零的有理数T,f(x+T)=f(x)对x∈R恒成立,故③正确;
对于④,取x1=-
,x2=0,x3=
,可得A(-
,0)、B(0,1)、C(
,0)三点恰好构成等边三角形,故④正确.
综上所述,真命题是②③④,
故选:D.
∴当x为有理数时,f(f(x))=f(1)=1;当x为无理数时,f(f(x))=f(0)=1,
即不管x是有理数还是无理数,均有f(f(x))=1,故①错误;
对于②,因为有理数的相反数还是有理数,无理数的相反数还是无理数,
所以对任意x∈R,都有f(-x)=f(x),故②正确;
对于③,若x是有理数,则x+T也是有理数; 若x是无理数,则x+T也是无理数,
∴根据函数的表达式,任取一个不为零的有理数T,f(x+T)=f(x)对x∈R恒成立,故③正确;
对于④,取x1=-
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
综上所述,真命题是②③④,
故选:D.
点评:本题考查命题的真假判断与应用,着重考查狄利克雷函数表达式的理解与应用,考查函数的奇偶性、周期性,考查分析、探究能力,属于难题.

练习册系列答案
相关题目
已知集合A={0,1,2},B={1,2,3},则∁(AUB)(A∩B)=( )
| A、{0,3} |
| B、{1,2} |
| C、∅ |
| D、{0,1,2,3} |
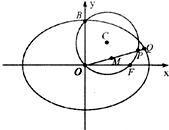 已知圆C经(x-1)2+(y-2)2=5经过椭圆E:
已知圆C经(x-1)2+(y-2)2=5经过椭圆E: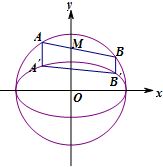 如图,设AB、A′B′分别是圆O:x2+y2=4和椭圆C:
如图,设AB、A′B′分别是圆O:x2+y2=4和椭圆C: