题目内容
设函数f(x)的定义域是(0,+∞),对任意正实数m,n恒有f(mn)=f(m)+f(n),且当x>1时,f(x)>0,f(2)=1
(Ⅰ) 求f(1),f(
),f(16)的值;
(Ⅱ) 求证:f(x)在(0,+∞)上是增函数;
(Ⅲ) 求方程4sinx=f(x)的根的个数.
(Ⅰ) 求f(1),f(
| 1 |
| 2 |
(Ⅱ) 求证:f(x)在(0,+∞)上是增函数;
(Ⅲ) 求方程4sinx=f(x)的根的个数.
考点:根的存在性及根的个数判断,函数单调性的判断与证明,函数的值
专题:函数的性质及应用
分析:(Ⅰ)利用赋值法,对于任意正实数m,n恒有f(mn)=f(m)+f(n),可令m=n=1,先求出f(1);然后令m=2 n=
,即可求出f(
)的值;再根据f(16)=2f(4)=4f(2),求得f(16)的值.
(Ⅱ)先在定义域内任取两个值x1,x2,并规定大小,然后判定出f(x1),与f(x2)的大小关系,根据单调增函数的定义可知结论.
(Ⅲ)分别画出y=4sinx的图象与y=f(x)的图象,结合图象以及函数的单调性判定出交点的个数即可.
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)先在定义域内任取两个值x1,x2,并规定大小,然后判定出f(x1),与f(x2)的大小关系,根据单调增函数的定义可知结论.
(Ⅲ)分别画出y=4sinx的图象与y=f(x)的图象,结合图象以及函数的单调性判定出交点的个数即可.
解答:
 解:(Ⅰ)令m=n=1,则f(1)=f(1)+f(1),∴f(1)=0.
解:(Ⅰ)令m=n=1,则f(1)=f(1)+f(1),∴f(1)=0.
令m=2 n=
,则f(1)=f(2×
)=0=f(2)+f(
),∴f(
)=-f(2)=-1.
f(16)=2f(4)=4f(2)=4.
(Ⅱ)设0<x1<x2,则
>1,∵当x>1时,f(x)>0,
∴f(
)>0,∴f(x2)=f(
•x1)=f(
)+f(x1),∴f(x2)-f(x1)=f(
)>0,
所以,f(x)在(0,+∞)上是增函数.
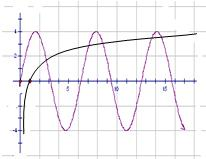
(Ⅲ) )∵y=4sinx的图象如右图所示
又f(4)=f(2×2)=2,f(16)=f(4×4)=4
由y=f(x)在(0,+∞)上单调递增,
且f(1)=0,f(16)=4可得y=f(x)的图象大致形状如右图所示,
由图象在[0,2π]内有1个交点,
在(2π,4π]内有2个交点,
在(4π,5π]内有2个交点,又5π<16<6π,
后面y=f(x)的图象均在y=4sinx图象的上方.
故方程4sinx=f(x)的根的个数为5个.
 解:(Ⅰ)令m=n=1,则f(1)=f(1)+f(1),∴f(1)=0.
解:(Ⅰ)令m=n=1,则f(1)=f(1)+f(1),∴f(1)=0.令m=2 n=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
f(16)=2f(4)=4f(2)=4.
(Ⅱ)设0<x1<x2,则
| x2 |
| x1 |
∴f(
| x2 |
| x1 |
| x2 |
| x1 |
| x2 |
| x1 |
| x2 |
| x1 |
所以,f(x)在(0,+∞)上是增函数.
(Ⅲ) )∵y=4sinx的图象如右图所示
又f(4)=f(2×2)=2,f(16)=f(4×4)=4
由y=f(x)在(0,+∞)上单调递增,
且f(1)=0,f(16)=4可得y=f(x)的图象大致形状如右图所示,
由图象在[0,2π]内有1个交点,
在(2π,4π]内有2个交点,
在(4π,5π]内有2个交点,又5π<16<6π,
后面y=f(x)的图象均在y=4sinx图象的上方.
故方程4sinx=f(x)的根的个数为5个.
点评:本题主要考查了抽象函数及其应用,以及函数单调性的判断与证明,体现了数形结合以及转化的数学思想,属于中档题.

练习册系列答案
相关题目
已知集合A={0,1,2},B={1,2,3},则∁(AUB)(A∩B)=( )
| A、{0,3} |
| B、{1,2} |
| C、∅ |
| D、{0,1,2,3} |
设集合S={x||x|<5},T={x|x2+4x-21<0},则S∩T=( )
| A、{x|-7<x<-5} |
| B、{x|3<x<5} |
| C、{x|-5<x<3} |
| D、{x|-7<x<5} |
已知函数f(x)=
,若关于x的方程f(x)=a(x+1)有三个不相等的实数根,则实数a的取值范围是( )
|
A、[
| ||
| B、(0,+∞) | ||
| C、C(0,1) | ||
D、(0,
|
已知定点A、B,且|AB|=2,动点P满足|PA|-|PB|=1,则点P的轨迹为( )
| A、双曲线 | B、双曲线一支 |
| C、两条射线 | D、一条射线 |
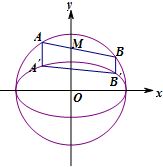 如图,设AB、A′B′分别是圆O:x2+y2=4和椭圆C:
如图,设AB、A′B′分别是圆O:x2+y2=4和椭圆C: