若数列{an}满足an+2=2•$\frac{{{a {n+1}}}}{a n}$.且a1=1.a2=2.则数列{an}的前2016项之积为( )A．22014B．22015C．22016D．22017 题目和参考答案——青夏教育精英家教网—

题目内容

18．若数列{a_n}满足a_n+2=2•$\frac{{{a_{n+1}}}}{a_n}$（n∈N*），且a₁=1，a₂=2，则数列{a_n}的前2016项之积为（　　）

A．

2²⁰¹⁴

B．

2²⁰¹⁵

C．

2²⁰¹⁶

D．

2²⁰¹⁷

分析利用递推关系可得：数列的前8项．利用周期性即可得出．

解答解：数列{a_n}满足a_n+2=2•$\frac{{{a_{n+1}}}}{a_n}$（n∈N*），且a₁=1，a₂=2，a₃=4，a₄=4，a₅=2，a₆=1，a₇=1，a₈=2，…
所以数列是周期为6的周期数列，a₁•a₂•a₃•a₄•a₅•a₆=2⁶．
则该数列前2016项积a₁•a₂…a₂₀₁₅•a₂₀₁₆=（a₁•a₂•a₃•a₄•a₅•a₆）³³⁶=2²⁰¹⁶．
故选：C．

点评本题考查了数列递推关系、数列周期性的应用，考查了推理能力与计算能力，属于中档题．

练习册系列答案

	A．	增函数		B．	减函数
	C．	先增后减函数		D．	与a，b有关，不能确定

9．已知函数f（x）=ax³+bx²-x+c（a，b，c∈R且a≠0）．
（1）若a=1，b=1，求函数f（x）的单调区间；
（2）若存在实数x₁，x₂（x₁≠x₂）满足f（x₁）=f（x₂），是否存在实数a，b，c，使f（x）在$\frac{{x}_{1}+{x}_{2}}{2}$处的切线斜率为0，若存在，求出一组实数a，b，c，否则说明理由．

6．已知S_n为等差数列{a_n}的前n项和，a₅=2，a_n-1+a_n+1=a₅a_n（n≥2）且a₃是a₁与-$\frac{8}{5}$的等比数列．
（1）求数列{a_n}的通项公式；
（2）若a₁为整数，b_n=$\frac{n}{（2{S}_{n}+23n）（n+1）}$，求数列{b_n}前n项和T_n．

13．下列四组函数，表示同一函数的是（　　）

	A．	$f（x）=\sqrt{x^2}，g（x）=x$		B．	$f（x）=\frac{{{x^2}-1}}{x-1}，g（x）=x+1$
	C．	$f（x）=\sqrt{{x^2}-4}，g（x）=\sqrt{x+2}\sqrt{x-2}$		D．	$f（x）=lg2-lgx，g（x）=lg\frac{2}{x}$

3．

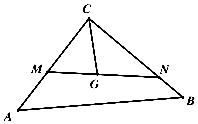如图，等腰直角三角形ABC，点G是△ABC的重心，过点G作直线与CA，CB两边分别交于M，N两点，且$\overrightarrow{CM}=λ\overrightarrow{CA}$，$\overrightarrow{CN}=μ\overrightarrow{CB}$，则λ+4μ的最小值为3．

10．过点（-1，-2）的直线l被圆x²+y²=3截得的弦长为$2\sqrt{2}$，则直线l的方程为x=-1或3x-4y-5=0．

7．由曲线y=x²与直线y=4x所围成的平面图形的面积是$\frac{32}{3}$．

8．已知函数f（x）=|x-1|．若|a|＜1，|b|＜1，且a≠0，求证：f（ab）＞|a|f（$\frac{b}{a}$）．

试题分类