题目内容
已知等比数列{an}的各项均为正数，a2＝8，a3＋a4＝48.
(1)求数列{an}的通项公式；
(2)设bn＝log4an.证明：{bn}为等差数列，并求{bn}的前n项和Sn.
(1)解
析：设等比数列{an}的公比为q，依题意q＞0.
因为a2＝8，a3＋a4＝48，所以a1q＝8，a1q2＋a1q3＝48.
两式相除得q2＋q－6＝0，解得q＝2(舍去q＝－3)．
所以a1＝
＝4.所以数列{an}的通项公式为an＝a1qn－1＝2n＋1(n∈N*)．
(2)证明：由(1)得bn＝log4an＝
，因为bn＋1－bn＝
＝
，
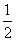所以数列{bn}是首项为1，公差为d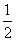＝的等差数列．
所以Sn＝nb1＋
d＝
(n∈N*)．
练习册系列答案
阅读快车系列答案
相关题目
________．
，其
中A，B，C是△ABC的内角．
in A＋sin C的取值范围．
是递增数列；④数列{an＋3nd}是递增数列．
，
，…，
，…是首项为1，公比为－
的等比数列，则a5＝________.
值；