题目内容
设函数y＝ax3＋bx2＋cx＋d的图象与y轴交点为P，且曲线在P点处的切线方程为12x－y－4＝0. 若函数在x＝2处取得极值0，试确定函数的解析式.
∵y＝ax3＋bx2＋cx＋d的图象与y轴的交点为P(0，d)，
又曲线在点P处的切线方程为y＝12x－4，P点坐标适合方程，从而d＝－4；
又切线斜率k＝12，故在x＝0处的导数y′|x＝0＝12而y′|x＝0＝c，从而c＝12；
又函数在x＝2处取得极值0，所以
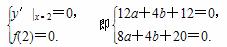解得a＝2，b＝－9，
所以所求函数解析式为y＝2x3－9x2＋12x－4.
练习册系列答案
相关题目
＝ad－bc，若数列{an}满足
＝1且
＝12(n∈N*)，则a3＝________，数列{an}的通项公式为an＝________.
上，α为曲线在P处的切线的倾斜角，则α的取值范围为( )
，n∈N＋，则数列{an}的前n项和是( )
；