Question

已知数列{a_n}的前n项和为S_n，且a_n是S_n与2的等差中项，而数列{b_n}的首项为1，b_n＋1－b_n－2＝0.

(1)求a₁和a₂的值；

(2)求数列{a_n}，{b_n}的通项a_n和b_n；

(3)设c_n＝a_n·b_n，求数列{c_n}的前n项和T_n.

Answer 1

解析：(1)因为a_n是S_n与2的等差中项，

所以S_n＝2a_n－2，所以a₁＝S₁＝2a₁－2，解得a₁＝2，a₁＋a₂＝S₂＝2a₂－2，解得a₂＝4；

(2)因为S_n＝2a_n－2，①

所以S_n－1＝2a_n－1－2(n≥2)，②

①－②得：a_n＝2a_n－2a_n－1，即a_n＝2a_n－1(n≥2，n∈N^*)，

因为a₁≠0，所以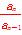＝2(n≥2，n∈N^*)，即数列{a_n}是等比数列．

因为a₁＝2，所以a_n＝a₁q^n－1＝2×2^n－1＝2ⁿ.

由已知得b_n＋1－b_n＝2，即数列{b_n}是等差数列，

又b₁＝1，所以b_n＝b₁＋(n－1)d＝1＋2(n－1)＝2n－1；

(3)由c_n＝a_n·b_n＝(2n－1)2ⁿ，

所以T_n＝a₁b₁＋a₂b₂＋…＋a_nb_n＝1×2＋3×2²＋5×2³＋…＋(2n－1)2ⁿ，③

所以2T_n＝1×2²＋3×2³＋…＋(2n－3)2ⁿ＋(2n－1)2^n＋1，④

③－④得：－T_n＝1×2＋(2×2²＋2×2³＋…＋2×2ⁿ)－(2n－1)2^n＋1，

即：－T_n＝1×2＋(2³＋2⁴＋…＋2^n＋1)－(2n－1)2^n＋1＝2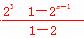＋－(2n－1)2^n＋1，

所以T_n＝(2n－3)2^n＋1＋6.