题目内容
设
=（2，2m-3，n+2），
=（6，2m-1，4n-2），且
∥
，则m+n= ．
| a |
| b |
| a |
| b |
考点：共线向量与共面向量
专题：空间向量及应用
分析：利用向量平行的坐标之间的关系解答．
解答：
解：∵
=（2，2m-3，n+2），
=（6，2m-1，4n-2），且
∥
，
∴
=
=
，
解得m=2，n=8；
∴m+n=10；
故答案为：10．
| a |
| b |
| a |
| b |
∴
| 2 |
| 6 |
| 2m-3 |
| 2m-1 |
| n+2 |
| 4n-2 |
解得m=2，n=8；
∴m+n=10；
故答案为：10．
点评：本题考查了空间向量平行的坐标关系，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
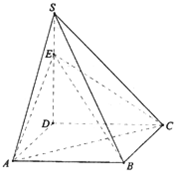如图，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=a，点E是SD上的点，且DE=λa（0＜λ≤1）．请利用空间向量解决下列问题：
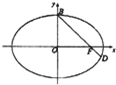如图，已知F是椭圆C的一个焦点，B是短轴的一个端点，线段BF的延长线交椭圆C于点D，且