题目内容
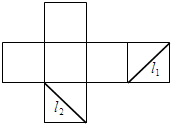
如图是正方体的侧面展开图,L1、L2是两条侧面对角线,则在正方体中,L1与L2( )

| A、互相平行 |
| B、相交 |
| C、异面且互相垂直 |
| D、异面且夹角为60° |
考点:空间中直线与直线之间的位置关系,异面直线及其所成的角
专题:空间位置关系与距离
分析:以涂有红色的正方形为下底面,并且使l1所在侧面正对着我们,可得l1与l2是相交直线.
解答:
解:如图,以涂有红色的正方形为下底面,
并且使l1所在侧面正对着我们,
可得l2所在的面是上底面,且两条直线有一个公共点
∴在正方体中,l1与l2是相交直线.
故选:B.

并且使l1所在侧面正对着我们,
可得l2所在的面是上底面,且两条直线有一个公共点
∴在正方体中,l1与l2是相交直线.
故选:B.
点评:本题给出正方体侧面展开图,叫们还原成立体图形并求空间直线所成的角,着重考查了正方体的性质和空间直线所成角的定义等知识,属于基础题.

练习册系列答案
相关题目
如果用反证法证明“数列{an}的各项均小于2”,那么应假设( )
| A、数列{an}的各项均大于2 |
| B、数列{an}的各项均大于或等于2 |
| C、数列{an}中存在一项ak,ak>2 |
| D、数列{an}中存在一项ak,ak≥2 |
已知等差数列{an},an=2n-19,那么这个数列的前n项和Sn( )
| A、有最小值且是整数 |
| B、有最小值且是分数 |
| C、有最大值且是整数 |
| D、有最大值且是分数 |
已知x,y满足约束条件
,则目标函数z=2x+y的最大值是( )
|
A、
| ||
B、2
| ||
C、
| ||
D、2
|
抛物线y=-
x2的焦点坐标为( )
| 1 |
| 4 |
A、(-
| ||
B、(
| ||
| C、(0,1) | ||
| D、(0,-1) |