题目内容
已知等差数列{an}，an=2n-19，那么这个数列的前n项和Sn（ ）
| A、有最小值且是整数 |
| B、有最小值且是分数 |
| C、有最大值且是整数 |
| D、有最大值且是分数 |
考点：等差数列的前n项和
专题：等差数列与等比数列
分析：利用等差数列的通项公式和前n项和公式求解．
解答：
解：∵等差数列{an}，an=2n-19，
∴a1=2-19=-17，a2=4-19=-15，
∴d=-15+17=2，
∴Sn=-17n+
×2
=n2-18n
=（n-9）2-81，
∴这个数列的前n项和Sn有最小值-81．
故选：A．
∴a1=2-19=-17，a2=4-19=-15，
∴d=-15+17=2，
∴Sn=-17n+
| n(n-1) |
| 2 |
=n2-18n
=（n-9）2-81，
∴这个数列的前n项和Sn有最小值-81．
故选：A．
点评：本题考查等差数列的前n项和的性质的应用，是基础题，解题时要注意配方法的合理运用．
练习册系列答案
相关题目
已知F1（-3，0），F2（3，0），是椭圆
+
=1（a＞b＞0）两个焦点，P在椭圆上，∠F1PF2=α，且当α=
时，△F1PF2的面积最大，则椭圆的标准方程为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 2π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若原点到直线ax+by+1=0的距离为
，则两圆（x-a）2+y2=1，x2+（y-b）2=1的位置关系是（ ）
| 1 |
| 2 |
| A、内切 | B、外切 | C、内含 | D、外离 |
已知i是虚数单位，则
=（ ）
| 2+i |
| 1+i |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图是正方体的侧面展开图，L1、L2是两条侧面对角线，则在正方体中，L1与L2（ ）
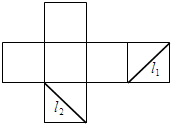
| A、互相平行 |
| B、相交 |
| C、异面且互相垂直 |
| D、异面且夹角为60° |
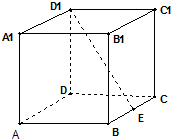如图在棱长为2的正方体ABCD-A1B1C1D1中E为BC的中点，点P在线段D1E上，点P到直线CC1的距离的最小值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
从0，1，2，3中选取三个不同的数字组成一个三位数，则不同的三位数有（ ）
| A、24个 | B、20个 |
| C、18个 | D、15个 |