题目内容
已知f(x)=mlnx-
x(m∈R),g(x)=2cos2x+sinx+a.
(Ⅰ)求函数f(x)的单调区间;
〔Ⅱ)当m=
时,对于任意x1∈[
,e],总存在x2∈[0,
],使得f(x1)≤g(x2)成立,求实数a的取值范围.
| 1 |
| 2 |
(Ⅰ)求函数f(x)的单调区间;
〔Ⅱ)当m=
| 1 |
| 2 |
| 1 |
| e |
| π |
| 2 |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(I)利用导数的运算法则可得:f′(x)=
-
=
(x>0).对m分类讨论:当m≤0时,当m>0时,即可得出其单调区间.
(II)对于任意x1∈[
,e],总存在x2∈[0,
],使得f(x1)≤g(x2)成立f(x)max?≤g(x)max.利用(I)的结论可得f(x)的最大值,利用二次函数的单调性可得g(x)的最大值.
| m |
| x |
| 1 |
| 2 |
| 2m-x |
| 2x |
(II)对于任意x1∈[
| 1 |
| e |
| π |
| 2 |
解答:
解:(I)f′(x)=
-
=
(x>0).
当m≤0时,f′(x)≤0,此时函数在(0,+∞)单调递减.
当m>0时,由f′(x)=0,解得x=2m.
令f′(x)>0,解得0<x<2m,此时函数f(x)单调递增;令f′(x)<0,解得2m<x,此时函数f(x)单调递减.
∴函数f(x)的单调递增区间为(0,2m),单调递减区间为(2m,+∞).
(II)对于任意x1∈[
,e],总存在x2∈[0,
],使得f(x1)≤g(x2)成立f(x)max?≤g(x)max.
当m=
时,f(x)=
lnx-
x,由(I)可知:当x∈[
,1]时,函数f(x)单调递增;
当x∈[1,e]时,函数f(x)单调递减.
∴当x=1时,函数f(x)取得最大值,f(x)max=f(1)=-
.
当x∈[0,
]时,sinx∈[0,1].
g(x)=2cos2x+sinx+a=2(1-sin2x)+sinx+a=-2sin2x+sinx+2+a=-2(sinx-
)2+
+a.
∴当sinx=
时,g(x)max=g(
)=a+
.
∴-
≤a+
,解得a≥-
.
∴实数a的取值范围是[-
,+∞).
| m |
| x |
| 1 |
| 2 |
| 2m-x |
| 2x |
当m≤0时,f′(x)≤0,此时函数在(0,+∞)单调递减.
当m>0时,由f′(x)=0,解得x=2m.
令f′(x)>0,解得0<x<2m,此时函数f(x)单调递增;令f′(x)<0,解得2m<x,此时函数f(x)单调递减.
∴函数f(x)的单调递增区间为(0,2m),单调递减区间为(2m,+∞).
(II)对于任意x1∈[
| 1 |
| e |
| π |
| 2 |
当m=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| e |
当x∈[1,e]时,函数f(x)单调递减.
∴当x=1时,函数f(x)取得最大值,f(x)max=f(1)=-
| 1 |
| 2 |
当x∈[0,
| π |
| 2 |
g(x)=2cos2x+sinx+a=2(1-sin2x)+sinx+a=-2sin2x+sinx+2+a=-2(sinx-
| 1 |
| 4 |
| 17 |
| 8 |
∴当sinx=
| 1 |
| 4 |
| 1 |
| 4 |
| 17 |
| 8 |
∴-
| 1 |
| 2 |
| 17 |
| 8 |
| 21 |
| 8 |
∴实数a的取值范围是[-
| 21 |
| 8 |
点评:本题考查了利用导数研究函数的单调性极值与最值、二次函数的单调性、恒成立问题的等价转化方法,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
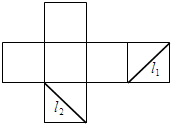
如图是正方体的侧面展开图,L1、L2是两条侧面对角线,则在正方体中,L1与L2( )

| A、互相平行 |
| B、相交 |
| C、异面且互相垂直 |
| D、异面且夹角为60° |
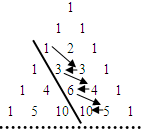 如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10…,记其前n项和为Sn,则S41的值为
如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10…,记其前n项和为Sn,则S41的值为