题目内容
已知函数f(x)=sinxcosx-
sin2x+2sin(x+
)cosx.
(1)求f(x)的周期;
(2)求f(x)的递减区间;
(3)说明f(x)的图象可由y=sin2x的图象经过怎样的变换得到.
| 3 |
| π |
| 3 |
(1)求f(x)的周期;
(2)求f(x)的递减区间;
(3)说明f(x)的图象可由y=sin2x的图象经过怎样的变换得到.
考点:函数y=Asin(ωx+φ)的图象变换,正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)由条件利用查三角恒等变换化简函数的解析式为f(x)=2sin(2x+
),可得它的周期.
(2)令2kπ+
≤2x+
≤2kπ+
,k∈z,求得x的范围,可得函数的减区间.
(3)根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
| π |
| 3 |
(2)令2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
(3)根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答:
解:(1)f(x)=sinxcosx-
sin2x+2sin(x+
)cosx
=sinxcosx-
sin2x+2(
sinx+
cosx)cosx=2sinxcosx+
cos2x
=2sin(2x+
),
故函数的周期为T=
=π.
(2)令2kπ+
≤2x+
≤2kπ+
,k∈z,求得kπ+
≤x≤kπ+
,
故函数的减区间为[kπ+
,kπ+
],k∈z.
(3)由y=sin2x的图象向左平移
个单位可得函数y=sin2(x+
)=sin(2x+
)的图象,
再把所得图象上点的纵坐标变为原来的2倍,可得函数f(x)=2sin(2x+
)的图象.
| 3 |
| π |
| 3 |
=sinxcosx-
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
=2sin(2x+
| π |
| 3 |
故函数的周期为T=
| 2π |
| 2 |
(2)令2kπ+
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
故函数的减区间为[kπ+
| π |
| 12 |
| 7π |
| 12 |
(3)由y=sin2x的图象向左平移
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
再把所得图象上点的纵坐标变为原来的2倍,可得函数f(x)=2sin(2x+
| π |
| 3 |
点评:本题主要考查三角恒等变换,函数y=Asin(ωx+φ)的周期性,正弦函数的减区间、函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
下面对相关系数r描述正确的是( )
| A、r>0表两个变量负相关 |
| B、r>1表两个变量正相关 |
| C、r 只能大于零 |
| D、|r|越接近于零,两个变量相关关系越弱 |
如图是正方体的侧面展开图,L1、L2是两条侧面对角线,则在正方体中,L1与L2( )
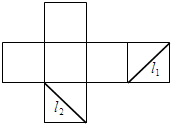

| A、互相平行 |
| B、相交 |
| C、异面且互相垂直 |
| D、异面且夹角为60° |
函数y=x+
(x>2)的最小值为( )
| 1 |
| x-2 |
| A、1 | B、2 | C、3 | D、4 |
从0,1,2,3中选取三个不同的数字组成一个三位数,则不同的三位数有( )
| A、24个 | B、20个 |
| C、18个 | D、15个 |