题目内容
已知点P是抛物线y2=4x上的一个动点，则点P到点（1，1）的距离与P到该抛物线焦点的距离之和的最小值为（ ）
| A、4 | B、3 | C、2 | D、1 |
考点：抛物线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据抛物线方程求出焦点坐标和准线方程，再由抛物线的定义知：当P、Q和P在准线上的射影点A三点共线时，这个距离之和最小，即可得出结论．
解答：
解：∵抛物线方程为y2=4x，
∴2p=4，可得焦点为F（1，0），准线为x=-1
设P在抛物线准线l上的射影点为A点，Q（1，1）
则由抛物线的定义，可知当P、Q、A点三点共线时，点P到点（1，1）的距离与P到该抛物线焦点的距离之和最小，
∴最小值为1+1=2．
故选：C．
∴2p=4，可得焦点为F（1，0），准线为x=-1
设P在抛物线准线l上的射影点为A点，Q（1，1）
则由抛物线的定义，可知当P、Q、A点三点共线时，点P到点（1，1）的距离与P到该抛物线焦点的距离之和最小，
∴最小值为1+1=2．
故选：C．
点评：本题给出抛物线上的动点，求该点到定点Q和焦点F距离之和的最小值，着重考查了抛物线的定义和简单几何性质等知识，属于中档题．
练习册系列答案
三新快车金牌周周练系列答案
相关题目
下面对相关系数r描述正确的是（ ）
| A、r＞0表两个变量负相关 |
| B、r＞1表两个变量正相关 |
| C、r 只能大于零 |
| D、|r|越接近于零，两个变量相关关系越弱 |
已知曲线C的参数方程
（t为参数），C在点（1，1）处的切线为l，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，则l的极坐标方程为（ ）
|
A、ρ=
| ||||
B、ρsin（θ+
| ||||
C、ρsin（θ+
| ||||
D、ρ=sin（θ+
|
若原点到直线ax+by+1=0的距离为
，则两圆（x-a）2+y2=1，x2+（y-b）2=1的位置关系是（ ）
| 1 |
| 2 |
| A、内切 | B、外切 | C、内含 | D、外离 |
已知θ是钝角三角形中的最小角，则sin（θ+
）的取值范围是（ ）
| π |
| 3 |
A、（
| ||||
B、[
| ||||
C、（
| ||||
D、[
|
如图是正方体的侧面展开图，L1、L2是两条侧面对角线，则在正方体中，L1与L2（ ）
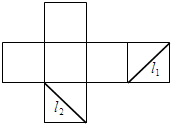
| A、互相平行 |
| B、相交 |
| C、异面且互相垂直 |
| D、异面且夹角为60° |
函数y=x+
（x＞2）的最小值为（ ）
| 1 |
| x-2 |
| A、1 | B、2 | C、3 | D、4 |