题目内容
对于函数f(x),若存在区间M=[a,b](a<b),使得{y|y=f(x),x∈M}=M,则称区间M为函数f(x)的一个“稳固区间”.现有四个函数:
①f(x)=ex;
②f(x)=x3;
③f(x)=sinx;
④f(x)=x2-2x+2.
其中存在“稳固区间”的函数有 .
①f(x)=ex;
②f(x)=x3;
③f(x)=sinx;
④f(x)=x2-2x+2.
其中存在“稳固区间”的函数有
考点:正弦函数的定义域和值域
专题:三角函数的图像与性质
分析:根据“稳定区间”的定义,我们要想说明函数存在“稳定区间”,我们只要举出一个符合定义的区间M即可,但要说明函数没有“稳定区间”,我们可以用反证明法来说明.由此对四个函数逐一进行判断,即可得到答案.
解答:
解::①对于函数f(x)=ex 若存在“稳定区间”[a,b],由于函数是定义域内的增函数,故有ea=a,eb=b,
即方程ex=x有两个解,即y=ex和y=x的图象有两个交点,这与即y=ex和y=x的图象没有公共点相矛盾,
故①不存在“稳定区间”.
②对于f(x)=x3 存在“稳定区间”,如 x∈[0,1]时,f(x)=x3 ∈[0,1].
③对于函数f(x)=sinx,若正弦函数存在等值区间[a,b],则在区间[a,b]上有sina=a,sinb=b,由正弦函数的值域知道[a,b]⊆[-1,1],但在区间]⊆[-1,1]上仅有sin0=0,所以函数f(x)=sinx没有“稳固区间”.
对于④f(x)=x2-2x+2,存在“稳定区间”,如 x∈[1,2]时,f(x)∈[1,2].
故答案为:②④.
即方程ex=x有两个解,即y=ex和y=x的图象有两个交点,这与即y=ex和y=x的图象没有公共点相矛盾,
故①不存在“稳定区间”.
②对于f(x)=x3 存在“稳定区间”,如 x∈[0,1]时,f(x)=x3 ∈[0,1].
③对于函数f(x)=sinx,若正弦函数存在等值区间[a,b],则在区间[a,b]上有sina=a,sinb=b,由正弦函数的值域知道[a,b]⊆[-1,1],但在区间]⊆[-1,1]上仅有sin0=0,所以函数f(x)=sinx没有“稳固区间”.
对于④f(x)=x2-2x+2,存在“稳定区间”,如 x∈[1,2]时,f(x)∈[1,2].
故答案为:②④.
点评:本题考查的知识点是函数的概念及其构造要求,在说明一个函数没有“稳定区间”时,利用函数的性质、图象结合反证法证明是解答本题的关键,属于基础题.

练习册系列答案
相关题目
三个平面最多可以把空间分成( )
| A、4部分 | B、6部分 |
| C、7部分 | D、8部分 |
下面对相关系数r描述正确的是( )
| A、r>0表两个变量负相关 |
| B、r>1表两个变量正相关 |
| C、r 只能大于零 |
| D、|r|越接近于零,两个变量相关关系越弱 |
如图是正方体的侧面展开图,L1、L2是两条侧面对角线,则在正方体中,L1与L2( )
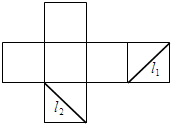

| A、互相平行 |
| B、相交 |
| C、异面且互相垂直 |
| D、异面且夹角为60° |