题目内容
若函数f(x)=4x-k•2x+k+3有唯一零点,则实数k的取值范围是 .
考点:函数的零点
专题:函数的性质及应用
分析:设t=2x,则t>0,将函数f(x)转化为y=g(t)=t2-k•t+k+3,利用二次函数的图象和性质进行求解即可.
解答:
解:设t=2x,则t>0,
则函数f(x)等价为y=g(t)=t2-k•t+k+3,在t>0时有唯一零点,
若△=0时,有对称轴x=-
=
>0,
即
,
∴
,解得k=6.
若△>0,即k>6或k<-2时,
满足g(0)<0,
即g(0)=k+3<0,
解得k<-3,
此时k<-3.
综上:实数k的取值范围是(-∞,-3)∪{6}.
故答案为:(-∞,-3)∪{6}.
则函数f(x)等价为y=g(t)=t2-k•t+k+3,在t>0时有唯一零点,
若△=0时,有对称轴x=-
| -k |
| 2 |
| k |
| 2 |
即
|
∴
|
若△>0,即k>6或k<-2时,
满足g(0)<0,
即g(0)=k+3<0,
解得k<-3,
此时k<-3.
综上:实数k的取值范围是(-∞,-3)∪{6}.
故答案为:(-∞,-3)∪{6}.
点评:本题主要考查函数零点的应用,利用换元法将函数转化为关于t的一元二次函数是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
条件p:2x≥(
)x,条件q:x2≥-x,则p是q的( )
| 1 |
| 2 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 某几何体的三视图如所示,该几何体的体积为( )
某几何体的三视图如所示,该几何体的体积为( )| A、20 | ||
B、
| ||
| C、56 | ||
| D、60 |
在区间[0,1]上任取两个数a,b,则函数f(x)=x2+ax+b2无零点的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
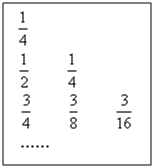 如图给出一个“直角三角形数阵”:满足每一列成等差数列;从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N+),则a86=( )
如图给出一个“直角三角形数阵”:满足每一列成等差数列;从第三行起,每一行的数成等比数列,且每一行的公比相等,记第i行第j列的数为aij(i≥j,i,j∈N+),则a86=( )A、
| ||
B、
| ||
C、
| ||
D、
|
不等式
≥3的解集为 ( )
| 2x+1 |
| x |
| A、[-1,0) |
| B、[-1,+∞) |
| C、(0,1] |
| D、(-∞,-1]∪(0,+∞) |
 一个正三棱柱的三视图如图所示,则a=
一个正三棱柱的三视图如图所示,则a= 如图△ABC的三个顶点都在⊙O上,∠BAC的平分线与BC边和⊙O分别交于点D、E.
如图△ABC的三个顶点都在⊙O上,∠BAC的平分线与BC边和⊙O分别交于点D、E.