题目内容
 如图△ABC的三个顶点都在⊙O上,∠BAC的平分线与BC边和⊙O分别交于点D、E.
如图△ABC的三个顶点都在⊙O上,∠BAC的平分线与BC边和⊙O分别交于点D、E.(1)指出图中相似的三角形,并说明理由;
(2)若EC=4,DE=2,求AD的长.
考点:相似三角形的判定
专题:直线与圆
分析:(1)利用角平分线的性质可得∠BAE=∠CAE.又∠B与∠AEC都对应
,可得∠B=∠AEC.利用对顶角可得∠ADB=∠CDE.利用相似三角形的判定即可得出.
(2)利用相似三角形的性质△AEC∽△CED,可得
=
,代入即可得出.
 |
| AC |
(2)利用相似三角形的性质△AEC∽△CED,可得
| AE |
| CE |
| CE |
| DE |
解答:
解:(1)∵AE平分∠BAC,∴∠BAE=∠CAE.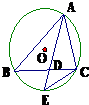
又∠B与∠AEC都对应
,∴∠B=∠AEC.
又∠ADB=∠CDE.
∴△ABD∽△AEC∽△CED.
(2)∵△AEC∽△CED,∴
=
,
∴
=
,解得AE=8.
∴AD=AE-DE=8-2=6.

又∠B与∠AEC都对应
 |
| AC |
又∠ADB=∠CDE.
∴△ABD∽△AEC∽△CED.
(2)∵△AEC∽△CED,∴
| AE |
| CE |
| CE |
| DE |
∴
| AE |
| 4 |
| 4 |
| 2 |
∴AD=AE-DE=8-2=6.
点评:本题考查了角平分线的性质、同弧所对的圆周角相等、对顶角相等、相似三角形的判定与性质等基础知识与基本技能方法,属于基础题.

练习册系列答案
相关题目
已知loga
<1,则a的取值范围是( )
| 2 |
| 5 |
A、0<a<
| ||
B、a<
| ||
C、
| ||
D、0<a<
|
下表显示出函数y随自变量x变化的一组数据,由此可判断它最可能的函数模型为( )
| x | -2 | -1 | 0 | 1 | 2 | 3 | ||
| y |
|
0.26 | 1.11 | 3.96 | 16.05 | 63.98 |
| A、一次函数模型 |
| B、二次函数模型 |
| C、指数函数模型 |
| D、对数函数模型 |
| ln2 |
| 2 |
| ln3 |
| 3 |
| ln5 |
| 5 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|