Question

在区间[0，1]上任取两个数a，b，则函数f（x）=x²+ax+b²无零点的概率为（　　）

• A、

  1

  2

• B、

  2

  3

• C、

  3

  4

• D、

  1

  4

Answer 1

考点：几何概型

专题：概率与统计

分析：在区间[0，1]上任取两个数a，b，函数f（x）=x²+ax+b²无零点?x²+ax+b²=0无实数根，a，b∈[0，1]?△=a²-4b²＜0，a，b∈[0，1]．画出可行域，利用几何概率的计算公式即可得出．

解答： 解：在区间[0，1]上任取两个数a，b，函数f（x）=x²+ax+b²无零点?x²+ax+b²=0无实数根，a，b∈[0，1]?△=a²-4b²＜0，a，b∈[0，1]．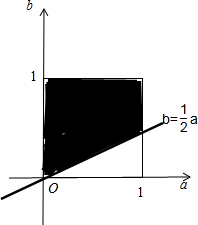
由约束条件

a，b∈[0，1] a2＜4b2

，画出可行域：
∴函数f（x）=x²+ax+b²无零点的概率P=1-

1

2

×1×

1

2

=

3

4

．
故选C．

点评：本题考查了线性规划的有关知识、几何概型的计算公式，属于基础题．