题目内容
如图，圆O1与圆O2的半径都是1，|O1O2|＝4，过动点P分别作圆O1，圆O2的切线PM，PN(M，N分别为切点)，使得|PM|＝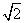
|PN|.试建立适当的坐标系，并求动点 P的轨迹方程．
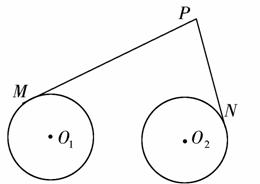
解析：以直线O1O2为x轴，线段O1O2的垂直平分线为y轴，建立平面直角坐标系，则两圆心分别为O1(－2,0)，O2(2,0)．
设P(x，y)，则|PM|2＝|O1P|2－|O1M|2＝(x＋2)2＋y2－1，
同理|PN|2＝(x－2)2＋y2－1.
∵|PM|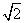＝|PN|，
∴(x＋2)2＋y2－1＝2[(x－2)2＋y2－1]，
即x2－12x＋y2＋3＝0，即(x－6)2＋y2＝33.这就是动
点P的轨迹方程．
练习册系列答案
相关题目
.
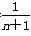(n∈N*)与椭圆C在第一象限内相交于点An(xn，yn)，记an＝
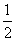x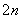
，试证明：对∀n∈N*
，a1·a2·…·an＞
|
CA|＝2，AC⊥CB，D，E分别是棱AC，B1C1的中点，求DE的长度．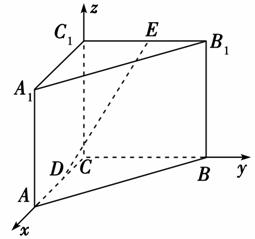
.设P为直线l上的点，过点P作抛物线C的两条切线PA，PB，其中A，B为切点．
B．1 C.
D
.
＝2
，则点C的轨迹是( )