题目内容
根据下列条件求椭圆的标准方程:
(1)焦点在x轴,两准线间的距离为
,焦距为2
;
(2)已知P点在以坐标轴为对称轴的椭圆上,点P 到两焦点的距离分别为
和
,过P点作长轴的垂线恰好过椭圆的一个焦点.
(1)焦点在x轴,两准线间的距离为
18
| ||
| 5 |
| 5 |
(2)已知P点在以坐标轴为对称轴的椭圆上,点P 到两焦点的距离分别为
4
| ||
| 3 |
2
| ||
| 3 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(1)据题意列出关于a,b,c的方程组,求出a,b,c,写出椭圆的方程;
(2)利用椭圆的定义及勾股定理列出方程组,求出a,b,c写出椭圆的方程.
(2)利用椭圆的定义及勾股定理列出方程组,求出a,b,c写出椭圆的方程.
解答:
解:(1)据题意
解得a=3,c=
,
∴a2=9,b2=a2-c2=4
∴椭圆的标准方程:
+
=1
(2)据题意得2a=
+
=2
,
∴a=
,
又∵(
)2=4c2+(
)2
解得c2=
∴b2=a2-c2=
∴椭圆的标准方程:
+
=1或
+
=1
|
解得a=3,c=
| 5 |
∴a2=9,b2=a2-c2=4
∴椭圆的标准方程:
| x2 |
| 9 |
| y2 |
| 4 |
(2)据题意得2a=
4
| ||
| 3 |
2
| ||
| 3 |
| 5 |
∴a=
| 5 |
又∵(
4
| ||
| 3 |
2
| ||
| 3 |
解得c2=
| 5 |
| 3 |
∴b2=a2-c2=
| 10 |
| 3 |
∴椭圆的标准方程:
| x2 |
| 5 |
| y2 | ||
|
| y2 |
| 5 |
| x2 | ||
|
点评:本题考查椭圆方程的定义及有关性质,椭圆中三个参数的关系,属于一道中档题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
已知双曲线的方程为
-
=1,点A,B在双曲线的右支上,线段AB经过双曲线的右焦点F2,|AB|=m,F1为另一焦点,则△ABF1的周长为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、2a+2m | B、a+m |
| C、4a+2m | D、2a+4m |
函数f(x)=x3-x-3的零点所在区间是( )
| A、[-1,0] |
| B、[0,1] |
| C、[1,2] |
| D、[2,3] |
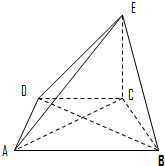 在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.
在如图所示的几何体中,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°,EC⊥平面ABCD,CB=CD=CE.