题目内容
4.给出下列四个命题:①函数f(x)=x+$\frac{9}{x}$的最小值为6;
②不等式$\frac{2x}{x+1}$<1的解集是{x|-1<x<1};
③若a>b>-1,则$\frac{a}{1+a}$>$\frac{b}{1+b}$;
④若a>b,c>d,则ac>bd.
所有正确命题的序号是②③.
分析 ①,函数f(x)=x+$\frac{9}{x}$的值域是[6,+∞)∪(-∞,-6];
②,不等式$\frac{2x}{x+1}$<1⇒$\frac{x-1}{x+1}<0$⇒-1<x<1;
③,由 a>b>-1⇒a+1>b+1>0⇒$0<\frac{1}{a+1}<\frac{1}{b+1}$⇒$\frac{a}{1+a}$>$\frac{b}{1+b}$;
④,当a>b>0,c>d>0时,才有ac>bd.
解答 解:对于①,函数f(x)=x+$\frac{9}{x}$的值域是[6,+∞)∪(-∞,-6],故错;
对于②,不等式$\frac{2x}{x+1}$<1⇒$\frac{x-1}{x+1}<0$⇒-1<x<1,故正确;
对于③,由 a>b>-1⇒a+1>b+1>0∴$\frac{a}{1+a}$-$\frac{b}{1+b}$=$\frac{a(1+b)-b(1+a)}{(1+a)(1+b)}=\frac{a-b}{(1+a)(1+b)}>0$,故正确;
对于④,当a>b>0,c>d>0时,才有ac>bd,故错.
故答案为:②③
点评 本题考查了命题真假的判定,属于基础题.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
19.下列各组函数中,表示同一函数的一组是( )
| A. | f(x)=$\frac{1}{x-1}$,g(x)=$\frac{x+1}{{x}^{2}-1}$ | B. | f(x)=|x+1|,g(x)=$\sqrt{{x}^{2}+2x+1}$ | ||
| C. | f(x)=x0,g(x)=1 | D. | f(x)=3x+2(x≥0),g(x)=2+3x |
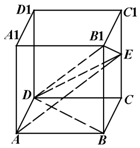 在正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.
在正方体ABCD-A1B1C1D1中,设E是棱CC1的中点.