题目内容
9.(1)求定积分${∫}_{-2}^{1}$|x2-2|dx的值;(2)若复数z1=a+2i(a∈R),z2=3-4i,且$\frac{{z}_{1}}{{z}_{2}}$为纯虚数,求|z1|
分析 (1)对x分类讨论,利用微积分基本定理即可得出.
(2)利用复数的运算法则、纯虚数的定义即可得出.
解答 解:(1)${∫}_{-2}^{1}$|x2-2|dx=${∫}_{-2}^{-\sqrt{2}}({x}^{2}-2)dx$+${∫}_{-\sqrt{2}}^{1}$(2-x2)dx=$(\frac{{x}^{3}}{3}-2x){|}_{-2}^{-\sqrt{2}}$+$(2x-\frac{{x}^{3}}{3}){|}_{-\sqrt{2}}^{1}$=$\frac{8}{3}\sqrt{2}$+$\frac{1}{3}$.
(2)∵$\frac{{z}_{1}}{{z}_{2}}$=$\frac{a+2i}{3-4i}$=$\frac{(a+2i)(3+4i)}{(3-4i)(3+4i)}$=$\frac{3a-8}{25}$+$\frac{(4a+6)}{25}$i为纯虚数,
∴$\frac{3a-8}{25}$=0,$\frac{(4a+6)}{25}$≠0,
解得a=$\frac{8}{3}$.
点评 本题考查了微积分基本定理、复数的运算法则、纯虚数的定义,考查了分类讨论方法、推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
19.已知长方体同一个顶点的三条棱长分别为2,3,4,则该长方体的外接球的表面积等于( )
| A. | 13π | B. | 25π | C. | 29π | D. | 36π |
20.一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的北偏东45°,则货轮的速度为( )
| A. | $20(\sqrt{3}+\sqrt{6})$海里/时 | B. | $20(\sqrt{6}-\sqrt{3})$海里/时 | C. | $20(\sqrt{2}+\sqrt{6})$海里/时 | D. | $20(\sqrt{6}-\sqrt{2})$海里/时 |
1.已知整数对排列如下:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4)则第60个整数对是( )
| A. | (5,11) | B. | (11,5) | C. | (7,5) | D. | (5,7) |
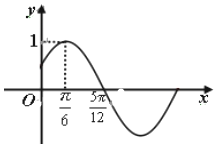 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$的部分图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$的部分图象如图所示.