题目内容
15.若集合A={x|x2-2x>0,x∈R},B={x||x+1|<0,x∈R},则A∩B=∅.分析 分别求出A与B中不等式的解集确定出A与B,找出A与B的交集即可.
解答 解:由集合A中的不等式变形得:x(x-2)>0,
解得:x<0或x>2,
即A=(-∞,0)∪(2,+∞);
由集合B中的不等式,根据绝对值的意义得:x∈∅,
即B=∅,
所以A∩B=∅.
故答案为:∅.
点评 本题考查了不等式的解法以及交集的运算问题,熟练掌握交集的定义是解题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
6.已知等差数列{an}的前三项分别为λ,6,3λ,前n项和为Sn,且Sk=165.
(1)求λ及k的值;
(2)设${b}_{n}=\frac{3}{2{S}_{n}}$,求数列{bn}的前n项和Tn.
(1)求λ及k的值;
(2)设${b}_{n}=\frac{3}{2{S}_{n}}$,求数列{bn}的前n项和Tn.
20.一货轮航行到M处,测得灯塔S在货轮的北偏东15°,与灯塔S相距20海里,随后货轮按北偏西30°的方向航行30分钟到达N处后,又测得灯塔在货轮的北偏东45°,则货轮的速度为( )
| A. | $20(\sqrt{3}+\sqrt{6})$海里/时 | B. | $20(\sqrt{6}-\sqrt{3})$海里/时 | C. | $20(\sqrt{2}+\sqrt{6})$海里/时 | D. | $20(\sqrt{6}-\sqrt{2})$海里/时 |
7.三棱锥A-BCD,顶点A在平面BCD内的射影为O,若AB=AC=AD,则点O为△BCD的( )
| A. | 内心 | B. | 外心 | C. | 中心 | D. | 垂心 |
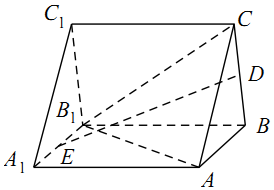 在如图所示的直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.
在如图所示的直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.