题目内容
19.下列各组函数中,表示同一函数的一组是( )| A. | f(x)=$\frac{1}{x-1}$,g(x)=$\frac{x+1}{{x}^{2}-1}$ | B. | f(x)=|x+1|,g(x)=$\sqrt{{x}^{2}+2x+1}$ | ||
| C. | f(x)=x0,g(x)=1 | D. | f(x)=3x+2(x≥0),g(x)=2+3x |
分析 根据两个函数的定义域相同、对应关系也相同,即可判断它们是同一个函数.
解答 解:对于A,f(x)=$\frac{1}{x-1}$的定义域为{x|x≠1},g(x)=$\frac{x+1}{{x}^{2}-1}$=$\frac{1}{x-1}$的定义域为{x|x≠±1},定义域不同,不是同一函数;
对于B,f(x)=|x+1|的定义域为R,g(x)=$\sqrt{{x}^{2}+2x+1}$=|x+1|的定义域是R,定义域相同,对应法则也相同,是同一函数;
对于C,f(x)=x0的定义域为{x|x≠0},g(x)=2logax的定义域为{x|x>0},两函数的定义域不同,不是同一函数;
对于D,f(x)=3x+2(x≥0)与g(x)=2+3x(x∈R)的定义域不相同,不是同一函数.
故选:B.
点评 本题考查了判断两个函数是否为同一函数的应用问题,是基础题目.

练习册系列答案
相关题目
7.三棱锥A-BCD,顶点A在平面BCD内的射影为O,若AB=AC=AD,则点O为△BCD的( )
| A. | 内心 | B. | 外心 | C. | 中心 | D. | 垂心 |
14.已知扇形OAB的面积为1,周长为4,则弦AB的长度为( )
| A. | 2 | B. | $\frac{2}{sin1}$ | C. | 2sin1 | D. | sin2 |
9.“sinα=cosα”是“$α=\frac{π}{4}$”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
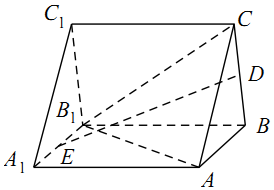 在如图所示的直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.
在如图所示的直三棱柱ABC-A1B1C1中,D,E分别是BC,A1B1的中点.